analiza matematyczna
lawenderr: Wyznacz wartosci (o ile istnieja) funkcji f: najwieksza i najmniejsza w podanym zbiorze:
| 1−x2 | |
| ,x nalezy do <−5;3) |
| x−3 | |
Wiem, ze najpierw trzeba obliczyc pochodna i ekstrema lokalne. Zrobilam tak, sprawdzilam czy
naleza one do zbioru. Obliczylam ich f(x) i f(−5) a odpowiedz i tak wychodzi mi zla.. nie wiem
co licze nie tak.
15 mar 18:41
Janek191:
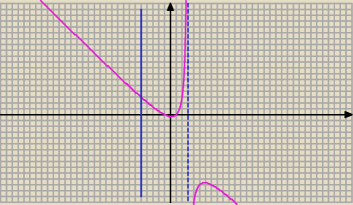
15 mar 18:49
lawenderr: Nie lubie nigdy korzystac wykresow, da sie to zrobic jakos algebraicznie wg sposobu, ktory
przedstawilam?
15 mar 18:52
Janek191:
| | − 2 x*( x − 3) − (1 − x2) | | − x2 + 6 x − 1 | |
f' ( x) = |
| = |
| = 0 ⇔ |
| | ( x − 3)2 | | ( x −3)2 | |
⇔ x
2 − 6 x + 1 = 0
Δ = 36 − 4*1*1 = 32 = 16*2 ⇒
√Δ = 4
√2
| | 6 − 4√2 | |
x1 = |
| = 3 − 2√2 x2 = 3 + 2√2 |
| | 2 | |
f(x
1) = y
min = ....
Nie ma wartości największej.
15 mar 18:56
5-latek: A co bedzie gdy przyjdzie zbadac przebieg zmiennosci funkcji i przyjdzie narysowac wykres ?
15 mar 18:58
Janek191:
Będą kłopoty

15 mar 19:08

