Okrąg (x-3)^2+(y-2)^2=25 przecina oś OX w punktach P i Q. Oblicz IPQI
Adam: Okrąg (x−3)2+(y−2)2=25 przecina oś OX w punktach P i Q. Oblicz IPQI
Obliczyłem środek i promień i nie wiem jak to rozwiązać.
15 mar 17:32
Janek191:
( x − 3)2 + ( y − 2)2 = 25
y = 0 − równanie osi OX
( x − 3)2 + 4 = 25
( x − 3)2 = 21
x − 3 = − √21 lub x − 3 = √21
x = 3 − √21 lub x = 3 + √21
y = 0
więc
I PQ I = ( 3 + √21) − ( 3 − √21) = 2√21
15 mar 17:37
Eta:
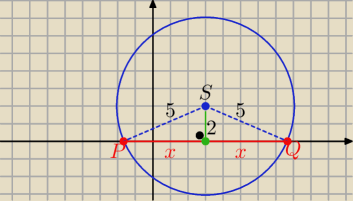
x=
√52−22=.........
|PQ|=2x=........
15 mar 17:40
Janek191:
15 mar 17:41
5-latek:
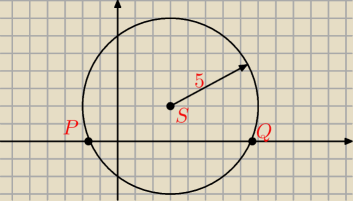
Nie ma potrzeby liczenia srodki i pronienia tylko nalezy odczytac bezposrednio z rownania
S=(3,2) (birzesz przeciwne znaki i promien r=5 bo w rownaniu jest r
2 a 5
2=25
Jesli ma przecinac OX to punkt przeciecia z oX bedzie mial wspolrzedne (x,0)
wiec wstaw do rownania okregu za y=0 i wylicz x
(x−3)
2+(0−2)
2=25
x
2−6x+9+4=25
dalej Ty
A |PQ| to dlugosc odcinka PQ
15 mar 17:41
Eta:
Pozdrawiam
Janek 
15 mar 17:42
Eta:
15 mar 17:42
Janek191:
Ale wysyp
15 mar 17:42
Eta:
Czyj sposób najkrótszy?
15 mar 17:43
Janek191:
Pozdrawiam Etę
Co tam w Rzeszowie ?
15 mar 17:43
Janek191:
Mój − bo bez rysunku szybciej
15 mar 17:44
5-latek:
Janek zobacz
15 mar 17:45
Eta:
Bazie kwitną nad Wisłokiem
15 mar 17:47
Janek191:
Toście hucznie witali mistrza polskiej ortografii ( bez Szoguna ? ) ?
15 mar 17:50
Janek191:
15 mar 17:54
Adam: Dzięki wszystkim
15 mar 18:14
5-latek:
15 mar 18:28