prostokąt Tak:

	15
sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy		. Oblicz jego obwód
	17

	1
skorzystałam z wzoru P =		x |AC| x |BD| x sinα i skoro przekątne są takie same to wyszło
	2

mi takie coś:

	1		15
60 =		x2 x|AC| x
	2		17

|AC|=|BD|=68 czy jest to dobrze zrobione? jeśli tak to co dalej, bo nie mam pojęcia?

Tak: up

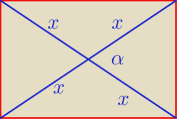
Janek191: P = 2 x²*sin α

	15
60 = 2 x2*
	17

	30		17
x2 =		= 30*		= 34
	15     17		15

x = √34

Janek191:

	225		64		8
cos α = √ 1 − sin2α = √ (1 −		) = √		=
	289		289		17

	8
b2 = x2 + x2 − 2 x2 cos α = 2*34 − 68*		= 68 − 32 = 36
	17

b = √36 = 6 =========== a² + b² = (2x)² = 4 x² a² + 36 = 4*34 a² = 136 − 36 = 100 a = 10 ====== Obwód prostokąta L = 2a + 2 b = 20 + 12 = 32 ======================

Tak: P = 2 x2*sin α − skąd ten wzór?

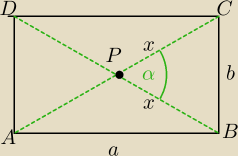
Mila: α− kąt ostry

	1
x=		p
	2

	15
sinα=
	17

a*b=60 P_▭=4*P_ΔBPC⇔

	1
4*(		*x*x*sinα)=60
	2

	15
x2*		=30
	17

	17
x2=30*
	15

x²=34 x=√34 p=|AC|=2√34 W ΔBPC: b²=x²+x²−2*x*x*cosα

	15
cos2α=1−(		)2
	17

	225
cos2α=1−
	289

	8
cosα=
	17

	8
b2=34+34−2*34*
	17

b²=68−32 b²=36 b=6 6²+a²=(2√34)² 36+a²=4*34 a²=100 a=10 spr. P=6*10=60 2a+2b=2*(6+10)=32 ===============

Tak: dzięki wielkie za odpowiedzi, ale skąd te wzory: kolejno P = 2 x2*sin α u Janka i 4*( *x*x*sinα) u Mili?

Janek191: Twierdzenie kosinusów

Janek191: Pole jednego Δ P = 0,5 x²*sin α pole prostokąta jest 4 razy większe, więc P₁ = 4*0,5 x² sin α = 2 x² sin α

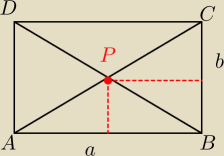
Mila: Przekątne dzielą prostokąt ( równoległobok) na 4 trójkąty o równych polach. P▭=a*b

	1		1		1		1
PΔABP=		*a*		b=		(a*b)=		P▭
	2		2		4		4

	1		1		1		1
PΔBCP=		b*		a=		(a*b)=		P▭
	2		2		4		4

Tak: dziękuję bardzo

Mila: