... Phoebe Campbell: Równanie a(x + 1) + x = b(x − 1) + 5, gdzie x jest niewiadomą, ma nieskończenie wiele rozwiązań. Znajdź liczby a i b. Moje obliczenia: a(x + 1) + x = b(x − 1) + 5 ax + a + x = bx − b + 5 x(a + 1 − b) = − a − b +5

	− a − b + 5
x=		dla a + 1 − b ≠ 0 → a − b ≠ −1
	a − b + 1

Skoro równanie ma nieskończenie wiele rozwiązań to na pewno x = 0, więc przyrównuje licznik do 0. − a − b + 5 = 0 a = 5 − b mianownik: a − b + 1 5 − b − b + 1 b = 3 a + b = 5 → a + 3 = 5 → a = 2 Więc a = 2 i b = 3... takie odpowiedzi mam też w książce, ale.. co z warunkiem a − b ≠ −1? Nie jest spełniony, więc dzielę przez zero... Jak powinienem to rozumieć?

Qulka: nie dzielisz tylko z tego miejsca x(a + 1 − b) = − a − b +5 rozważasz kiedy to jest nieskończenie wiele czyli dowolne x ano tylko wtedy kiedy (a + 1 − b) =0 i jednocześnie − a − b +5 =0

Phoebe Campbell: Czyli... nie wystarczy, że licznik będzie równy 0.. mianownik też musi być? To potem układam układ równań dla a + 1 − b = 0 i − a − b + 5 = 0 i wyliczam a i b?

Qulka: tak jeśli ax=b ma mieć nieskończenie wiele to a=0 i b=0 jeśli ma być sprzeczny to a=0 i b≠0 jeśli 1 rozwiązanie to a≠0 żeby można było podzielić

Phoebe Campbell: Okej, dzięki bardzo

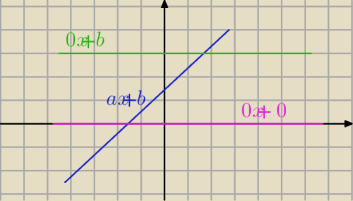
Qulka: rozwiązanie y=0 to przecięcie z osią OX dla a=0 i b=0 wszystkie x (fioletowa) dla a=0 i b≠0 nie ma takich (sprzeczne) (zielona) dla a≠0 jest jedno (niebieska)

Phoebe Campbell: Przerysuje sobie to do zeszytu, dzięki

Phoebe Campbell: Możesz Qulka sprawdzić? (a i b to parametry) a²(x − 1) − ab = b²(x + 1) + ab a²x − a² − ab = b²x + b² + ab a²x − b²x = b² + ab + a² + ab x(a² − b²) = a² + b² + ab x(a − b)(a + b) = (a + b)²

	(a + b)2		a + b
x =		=
	(a − b)(a + b)		a − b

nsk wiele rozwiązań dla a − b = 0 i a + b = 0 sprzeczne dla a − b = 0 i a + b ≠ 0 1 rozwiązanie dla a − b ≠ 0

Qulka: 1 rozwiązanie jeszcze dla a+b≠0

Qulka: tu ci się przypadkiem udało, ale nie dziel i nie skracaj

Qulka: x(a−2)(a−3)=(a−2)(b−3) ma nieskończenie wiele dla a=2 lub a=3 i b=3 jakbys skrócił znikłoby Ci a=2

Phoebe Campbell: 1 rozwiązanie będzie jeżeli a+b≠0 i a−b≠0? Jeżeli nie mam dzielić i skracać.. to jak to rozwiązać inaczej? I czemu nie mogę dzielić i skracać?

Qulka: bo dzielisz przez 0... masz analizować przypadki przed podzieleniem

Phoebe Campbell: Teraz dopiero zauważyłem Twój ostatni post.. czyli doprowadzam do ax + b i wtedy: nsk wiele dla a=0 i b=0 sprzeczne dla a=0 i b≠0 1 rozw dla a≠0 i b≠0?

Qulka: nie możesz dzielić przez 'a' skoro sprawdzasz, że a=0

Qulka: w 1 rozwiązanie tylko warunek dla a ≠0 b może być dowolne

Phoebe Campbell: Okej, dziękuje

Qulka: ale tak..taka analiza