xyz
gil: Przekątne trapezu dzielą go na cztery trójkąty. Pola trójkątów zawierających podstawy trapezu
są równe odpowiednio m2 i n2. Udowodnij ze pole trapezu jest równe (m+n)2
14 mar 21:35
Braun:
1. Rysunek
2.Trójkąty podobne
3. Skala podobieństwa
14 mar 21:37
Eta:
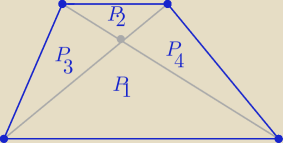
| P1 | |
| =k2 , k >0−− skala podobieństwa trójkątów o polach P1 −P2 |
| P2 | |
P(tr)=(k+1)2*P2
| | m2 | | m | |
k2= |
| ⇒ k= |
| i P2= n2 |
| | n2 | | n | |
| | m | |
P(tr)= ( |
| +1)2*n2 ⇒ P(tr)=(m+n)2 |
| | n | |
14 mar 22:19
Eta:
Drugi wzór: P(tr)= (√P1+√P2)2
to P(tr)= (m+n)2
14 mar 22:21
