monotoniczność ciągu arytm serkaz97: Ciąg (a_n) określony jest wzorem:

	49n2 − 25
(an)=
	(7n−5)(n+1)

a) zbadaj na podstawie definicji monotoniczność tego ciągu b)Pierwszy i czwarty wyraz ciągu (a_n) są równe odpowiednio pierwszemu i siódmemu wyrazowi arytmetycznego (b_n). Ile początkowych wyrazów ciągu (b_n) należy dodać, aby otrzymana suma była równa 163,8?

===:

	7n+5
an=
	n+1

... i teraz łatwiej

serkaz97: wychodzi ciąg malejący, ok, jak się zabrać do b)?

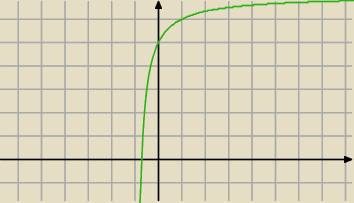
===: ...a niby dlaczego malejący ?

Janek191: Raczej rosnący

	7*( n + 1) − 2		2
an =		= 7 −
	n + 1		n + 1

serkaz97: dobra, zrobiłem błąd...

===: a₁=6 a₄=33/5 r_a=... b₁= b₇= r_b= itd −