Równanie okręgu Daniel: napisz równanie okręgu wpisanego w trójkąt, którego jeden bok jest zawarty w osi OX, a dwa pozostałe boki są zawarte w wykresie funkcji f(x) = −⁴₃IxI + 4

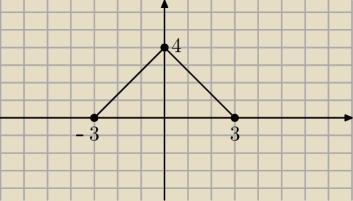
J: i działasz dalej

5-latek:

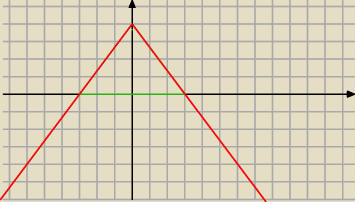
	4
Czerwony to wykres y=−		|x|+4
	3

Gdzie lezy srodek okregu wpisanego w trojkat ? Na promien jest wzor

Daniel: Dzięki bardzo

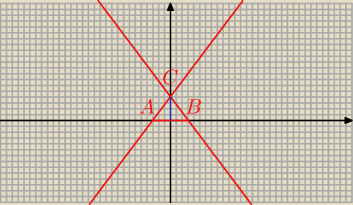
Janek191: x > 0

	4
f(x) = −		x + 4
	3

x < 0

	4
f(x) =		x + 4
	3

więc A = ( − 3, 0) B = ( 3, 0) I AB I = 3 − (−3) = 6

	√3
h = 6		= 3 √3
	2

zatem P_Δ = 0,5*6*3 √3 = 9√3 =====================

J: nie o pole trójkata chodziło

Janek191: Pomyłka C = ( 0 , 4) więc I AC I = I BC I = 5 P = 0,5 *6*4 = 12 Oblicz obwód

J: leipej ...

Daniel:

Janek191: L = 6 + 2*5 = 16 p = 8

	P		12
r =		=		= 1,5
	p		8

Janek191:

	1
S = ( 0, 1		)
	2

mleko: Dzięki za pomoc Janek

5-latek: A kolega J i ja CI nie pomagalismy?