jednokładność A: A(0−4) B(0,6) C(−4,4) Obrazem trójkąta ABC w jednokładności o środku S i skali k, k<0 jest trójkąt A'B'C' którego pole wynosi . Wiedząc dodatkowo, że C' (6¹₂,−3¹₂), oblicz skalę jednokładności i współrzędne punktu S. Wiem tylko że punkt S będzie się znajdował pomiędzy obiema figurami, ale poza tym, nie wiem jak się do tego zabrać.

Janek191: A ile wynosi pole ?

A: Oh, nie zauważyłam. Pole wynosi 5

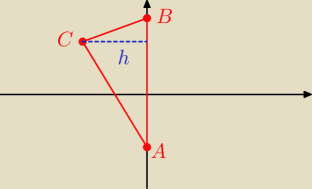
Janek191: Oblicz pole Δ ABC czyli P₁ Masz P₂ = 5 zatem

P2
	= k2 ⇒ k = ( bierzesz ze znakiem ujemnym)
P1

Janek191: cd. I AB I = 6 − (−4) = 10 h = I − 4 I = 4 P₁ = 0,5*10*4 = 20 więc

5		1		1
	=		= k2 ⇒ k = −		= − 0,5
20		4		2

A: No tak, rzeczywiście, dzięki.