proszę o rozwiązanie Michał: W trapez równoramienny o kącie ostrym którego miara wynosi 30⁰ wpisano okrąg o promieniu 3 Wyznacz promień okręgu opisanego na tym trapezie Zakoduj cyfry dziesiątek ,jedności i części dziesiętnych rozwinięcia dziesiętnego otrzymanego wyniku h = 2r r = 3 ⇒ h =6 c − ramię trapezu a − podstawa dłuższa b − podstawa krótsza

h
	= sin300 ⇒ c = 12 a+ b = 2c =24
c

nie wiem jak obliczyć promień okręgu opisanego na tym trapezie wynik to 134

Eta:

	a+b
a+b=12c=24 ⇒		=12
	2

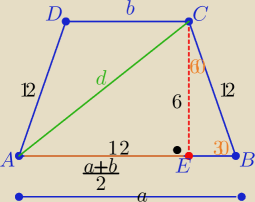
d=√144+36=6√5 z tw. sinusów w trójkącie AEC( bo okrąg opisany na trapezie jest też opisany na trójkącie AEC

	d
2R=		⇒ R=..........
	sin30o

i masz właściwą odp : i koduj.........

Eta: Poprawiam chochlika Z tw. sinusów w trójkącie ABC

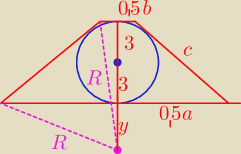
Janek191: cd. x² + 6² = c² x² = 144 − 36 = 108 = 36*3 x = 6√3 2 b + 2 x = = 2 c 2 b + 12√3 = 24 2 b = 24 − 12√3 ⇒ b = 12 − 6√3 0,5 b = 6 − 3√3 −−−−−−−−−−−−−− a = b + 2 x = 12 − 6√3 + 12√3 = 12 + 6√3 0,5 a = 6 + 3√3 −−−−−−−−−−−−−−−− R² = (0,5 a)² +y² R² = (0,5 b)² + ( 6 + y)² czyli porównując prawe strony otrzymamy ( 6 + 3√3)² + y² = ( 6 − 3√3)² + 36 + 12 y + y² 36 + 36√3 + 27 = 36 − 36√3 + 27 + 36 + 12 y 36√3 = 36 − 36√3 + 12 y 12 y = 72√3 − 36 y = 6√3 − 3 ========== zatem R² = (0,5 a)² + y² = ( 6 + 3√3)² + ( 6√3 − 3)² R² = 36 + 36√3 + 27 + 108 − 36√3 + 9 R² = 180 = 36*5 R = 6√5 ≈ 13,4 ==============

Eta: Ale się opisałeś .....

Janek191: Oliczyłem się , ale wyszło tyle samo

Eta: Do Rzeszowa ......też można dojechać z Krakowa przez Warszawę

Janek191: Tam powinien być pewnie Δ ABC ?

Janek191: Zgadza się

Eta: Poprawiłam chochlika 22:46

Janek191: Nie doczytałem

Mila: Dobranoc Państwu

Michał: dziękuję bardzo

Eta: Miłych snów

Eta: A już myślałam,że Michał śpi