. Darek: Proszę o pomoc z analityczną. Z punktu A=(5,0) poprowadzono styczne do okręgu o równaniu x²+y²=4. Wyznacz tangens kąta, pod którym przecinają się te styczne.

Braun: y=ax+b 0=5a+b ⇒b=−5a y=ax−5a −ax+y+5a=0

|−ax+y+5a|
	=2
√a2+1

|5a|
	=2 / √a2+1
√a2+1

|5a|=2√a²+1 /² 25a²=4a2+4 21a²=4

	2√21		2√21
a1=		lub a2=−
	21		21

	2√21		10√21
y1=		−
	21		21

	2√21		10√21
y2=−		+
	21		21

dalej dokończ sam, bo za dużo pisania jest =====================

prosta: a może tak: długość odcinka AP ( do punktu styczności )|AP| =√21

	2
tgβ=
	√21

	2tgβ
tgα=tg2β=
	1−tg2β

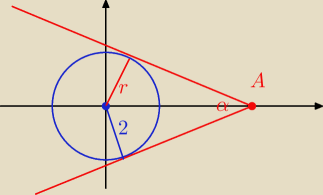Janek191: y = a x + b A = ( 5, 0) więc 0 = 5 a + b ⇒ b = − 5 a y = a x − 5 a = a*( x − 5) x² + y² = 4 −−−−−−−−−−−− x² + a²*( x − 5)² = 4 x² + a²( x² − 10 x + 25) − 4 = 0 x² + a² x² − 10a² x + 25 a² − 4 = 0 ( 1 + a²) x² − 10 a² x + 25a² − 4 = 0 Δ = 100 a⁴ − 4*( 1 + a²)*( 25 a² − 4) = 100a⁴ − 4*(25a² − 4 + 25 a⁴ − 4 a²) =

	4
= 100a4 − 100a4 − 84 a2 + 16 = − 84 a2 + 16 = 0 ⇔ a2 =
	21

	2		2
a1 =		a2 = −
	√21		√21

	a1 − a2		4 √21
tg α = I		I =
	1 + a1*a2		17

Braun: Nie lubię tej metody Janka, jestem za dużym leniuchem żeby to wszystko wymnażać i porządkować

Eta: |OA|=5 , |OB|=2

	α		2		α		4		√21
sin		=		, to cos		= p{1−		=
	2		5		2		25		5

	α		α		4√21
2sin		*cos		= sinα=
	2		2		5

	17
cosα= √1−sin2α=
	25

	4√21
to tgα= ........=
	17

Eta: @Braun A taką "lubisz" ?

Braun: O i jakie ładne rozwiązanie Cioci Ety. Ale dla myślących

Eta:

	α		4		√21
Poprawiam zapis : cos		=√1−		=
	2		25		5

Braun: Eta osobiście podziwiam Twój talent do planimetrii ! Oby więcej takich rozwiązań, a nie klepanie schematów

Eta: Jeszcze poprawiam chochlika

	4√21
sinα=
	25

Darek: Dziękuję