styczna do paraboli załamana: Dana jest parabola y=¹₆x² − ¹₂ Wyznacz równanie stycznej do tej paraboli, jeżeli styczna tworzy z osią OX kąt 120 stopni.

Karin: Tg120=a tg (180−120)=−tg60=−p {3} Styczna: y=ax+b ==> y=−p {3}x+b licze pochodna f (x)=1/3x F'(a)=xo 1/3 × (−p {3})=xo yo liczysz podstawiajac xo do wzoru f(x) (np) yo=−4/9 Do stycznej −4/9=p {3}x1/3×p {3}+b b=−13/9 Styczna y=p {3}x−13/9 Mam nadzieje ze dobrze

Mila:

	1		1
f(x)=		x2−
	6		2

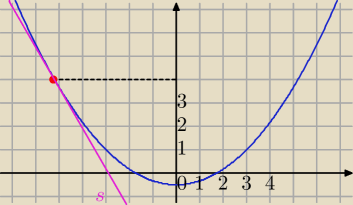
Styczna y=f'(x₀)x+b

	2
f'(x)=		x
	6

	1
f'(x)=		x
	3

tg(120^o)=f'(x₀) ============

1
	x0=−tg(60o)
3

1
	x0=−√3
3

x₀=−3√3

	1		1
f(−3√3)=		*(−3√3)2−		=4
	6		2

P=(−3√3,4) punkt styczności s: y=−√3x+b 4=−√3*(−3√3)+b⇔ 4=9+b, b=−5 Styczna: y=−√3x−5

prosta:

	1		1
f(x)=		x2−
	6		2

	1
f'(x)=		x i tg120o=−tg60o=−√3
	3

	1
szukamy punktu styczności:		x=−√3
	3

	1		1
x=−3√3 ⇒ y=		(−3√3)2−
	6		2

x=−3√3 , y=4 ⇒P(−3√3,4) równanie stycznej: y=−√3(x+3√3)+4

załamana: Każde z Was ma inny wynik

Mila: Musisz analizować.

Braun: Boże widzisz i nie grzmisz ! −√3*3√3+4=−5

załamana: ale ze mnie gapa

Mila: Ponadto wypada podziękować.

Eta: dla Mili

załamana: thanks