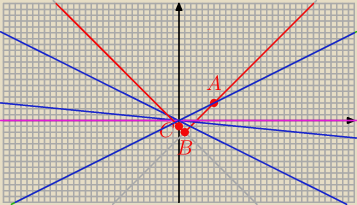
 1) Dla x ≥ 1 jest y = x − 1 − 2 = x − 3
2) Dla x < 1 jest y = − ( x − 1) − 2 = − x − 1
y = 2m x
Szukamy punktów wspólnych:
1) y = x − 3 i y = 2m x i x > 1
x − 3 = 2 m x
x − 2m x = 3
x*( 1 − 2m) = 3
1) Dla x ≥ 1 jest y = x − 1 − 2 = x − 3
2) Dla x < 1 jest y = − ( x − 1) − 2 = − x − 1
y = 2m x
Szukamy punktów wspólnych:
1) y = x − 3 i y = 2m x i x > 1
x − 3 = 2 m x
x − 2m x = 3
x*( 1 − 2m) = 3
| 3 | 1 | |||
x = | i x > 1 więc m ∊ ( − 1, | ) | ||
| 1 − 2m | 2 |
| 3 | 1 − 2m | 6m | ||||
y = | − 3* | = | ||||
| 1 − 2m | 1 − 2m | 1 − 2m |
| 3 | 6m | |||
A = ( | , | ) | ||
| 1 − 2m | 1 − 2m |
| 1 | 1 | |||
x = − | i x < 1 więc m∊ (−∞ , − 1) ∪ (− | , +∞ ) | ||
| 2m + 1 | 2 |
| 2m | ||
y = 2m x = − | ||
| 2m + 1 |
| 1 | 2m | |||
C = ( − | , − | ) | ||
| 2m + 1 | 2m + 1 |
| 1 | 1 | |||
oraz m ∊ ( − | , | ) | ||
| 2 | 2 |
| 2 + 2m | 2m + 2 | |||
BA = [ | , | ] | ||
| 1 − 2m | 1 − 2m |
| − 2m − 2 | 2m + 2 | |||
BC = [ | , | ] | ||
| 2m + 1 | 2m + 1 |
| ( 2 + 2m)2 | ||
P = 0,5 *I det ( BA, Bc ) I = | ; m ∊ ( − 0,5 ; 0,5 ) | |
| I 1 − 4 m2I |
 1) Dla x ≥ 1 jest y = x − 1 − 2 = x − 3
2) Dla x < 1 jest y = − ( x − 1) − 2 = − x − 1
y = 2m x
Szukamy punktów wspólnych:
1) y = x − 3 i y = 2m x i x > 1
x − 3 = 2 m x
x − 2m x = 3
x*( 1 − 2m) = 3
1) Dla x ≥ 1 jest y = x − 1 − 2 = x − 3
2) Dla x < 1 jest y = − ( x − 1) − 2 = − x − 1
y = 2m x
Szukamy punktów wspólnych:
1) y = x − 3 i y = 2m x i x > 1
x − 3 = 2 m x
x − 2m x = 3
x*( 1 − 2m) = 3
| 3 | 1 | |||
x = | i x > 1 więc m ∊ ( − 1, | ) | ||
| 1 − 2m | 2 |
| 3 | 1 − 2m | 6m | ||||
y = | − 3* | = | ||||
| 1 − 2m | 1 − 2m | 1 − 2m |
| 3 | 6m | |||
A = ( | , | ) | ||
| 1 − 2m | 1 − 2m |
| 1 | 1 | |||
x = − | i x < 1 więc m∊ (−∞ , − 1) ∪ (− | , +∞ ) | ||
| 2m + 1 | 2 |
| 2m | ||
y = 2m x = − | ||
| 2m + 1 |
| 1 | 2m | |||
C = ( − | , − | ) | ||
| 2m + 1 | 2m + 1 |
| 1 | 1 | |||
oraz m ∊ ( − | , | ) | ||
| 2 | 2 |
| 2 + 2m | 2m + 2 | |||
BA = [ | , | ] | ||
| 1 − 2m | 1 − 2m |
| − 2m − 2 | 2m + 2 | |||
BC = [ | , | ] | ||
| 2m + 1 | 2m + 1 |
| ( 2 + 2m)2 | ||
P = 0,5 *I det ( BA, Bc ) I = | ; m ∊ ( − 0,5 ; 0,5 ) | |
| I 1 − 4 m2I |