stereometria w optymalizacji Marta: z wycinka kola o promieniu 12 i kącie α utworzono stożek. wyznacz kąt α dla ktorego objętość stożka jest maksymalna

J: i z czym masz problem ?

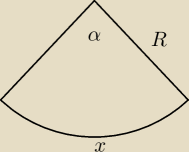
J: R = 12 , oblicz x jako funkcję kąta α

Marta: wyszło mi r=4√6 i α=30r alfa może być większe od 180?

J: co to jest r = 4√6 ?

	α
natomiast jest dobrze: r =		− promień podstawy stożka ,
	30

jeszcze potrzebna jest wysokość H

Marta: r to promień stożka, wyliczylam maksymalne r, bo jakbym podstawiala do wzoru α to wyszlyby ogromne liczby V=¹₃πr²√144−r²

J: to nic nie daje .. największe r nie gwarantuje maksymalnej objętości ( ze wzrostem r maleje wysokość) ikoniecznym jest znalezienie maksimum funkcj

pigor: ... , np. tak : niech α− miara kąta w radianach , r długość promienia podstawy stożka, to z warunków zadania ; 2πr= α*R=12α i H²=12²−r² i V_s(α)= ¹₃π r²H ⇒

	6
⇒ πr=6α i Vs(α)= 13π r2√122−r2, podstaw r=		α,
	π

i szukaj max, funkcji V_s(α)

Marta: Nie za bardzo rozumiem, wyliczylam maksimum funkcji, ale z parametrem r więc skoro mam r to nie

	α
wystarczy pomnożyć razy 30, nie wychodzi na to samo? Mam podstawiac pod r		i wrzucać
	30

to pod pietwiastek?

Marta: ok, dzięki pigor, tak jest chyba najłatwiej

J: mnie wyszło : r = ⁴√24 i wtedy: α = 30*⁴√24

Marta: Sposobem pigora wyszło mi tyle samo, co po podstawieniu pod r 4√6 mój sposób też jest dobry w takim razie J musisz mieć gdzieś błąd