 Witam,
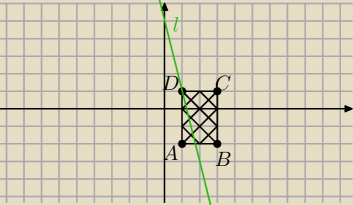
Prosta l przechodzi przez punkty P=(−1,9) i S=(2,−3). Prosta k ma równanie 2x−y+m−1=0. Znajdź
te wartości parametru m, aby punkt przecięcia prostych l i k należał do wnętrza prostokąta o
wierzchołkach A=(1,−2), B=(3,−2), C=(3,1), D=(1,1).
No więc mam pytanie, czy dobrze robię to zadanie.
1. wyznaczam równanie prostej l: y=−4x+5
2. przyrównuję ją do prostej k: y=2x+m−1
Witam,
Prosta l przechodzi przez punkty P=(−1,9) i S=(2,−3). Prosta k ma równanie 2x−y+m−1=0. Znajdź
te wartości parametru m, aby punkt przecięcia prostych l i k należał do wnętrza prostokąta o
wierzchołkach A=(1,−2), B=(3,−2), C=(3,1), D=(1,1).
No więc mam pytanie, czy dobrze robię to zadanie.
1. wyznaczam równanie prostej l: y=−4x+5
2. przyrównuję ją do prostej k: y=2x+m−1
| 6−m | 2m+9 | |||
3. wyliczam x= | i y= | |||
| 6 | 3 |
| 15 | ||
m∊<− | ;−3> | |
| 2 |


 , bo odpowiedź jednak nie taka jak powinna być
, bo odpowiedź jednak nie taka jak powinna być