Funkcja kwadratowa-przekształcenia oś OX,OY magda96: 1.Funkcja f dana jest wzorem f(x) =(x−2)² + 1. Wyznacz zbiór wartości funkcji g oraz równanie osi symetrii jej wykresu. a) g(x) = f(x+1) − 1 b) g(x) = 1 − f(2−x) 2. Wykres funkcji g jest symetryczny do wykresu funkcji f(x) = \frac{1}{2} x + 1 względem początku układu współrzędnych. Wyznacz wzór funkcji g. Naszkicuj wykresy obu funkcji i odczytaj rozwiązanie układu nierówności: (w klamrze) : f(x) ≤ 3 g(x)≥−2

Janek191: 1. f(x) = ( x − 2)² + 1 a) g(x) = f( x + 1) − 1 = ( x + 1 − 2)² + 1 − 1 = ( x − 1)² Oś symetrii x = 1 ZW = < 0 ; + ∞ )

magda96: Zadanie 2. Wykres funkcji g jest symetryczny do wykresu funkcji f(x) = ¹₂ x + 1 względem początku układu współrzędnych. Wyznacz wzór funkcji g. Naszkicuj wykresy obu funkcji i odczytaj rozwiązanie układu nierówności: (w klamrze) : f(x) ≤ 3 g(x)≥−2

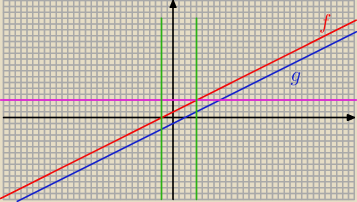
Janek191: z.2

	1
f( x) =		x + 1
	2

	1
g(x) =		x − 1
	2

magda96: A czy mogę prosić o wytłumaczenie, jak wyznacza się wzór funkcji symetrycznej wzgl. początku układu współrzędnych? NIe miałam z tym wcześniej do czynienia i nie wiem do końca jak to się robi.

Janek191:

	1
f(x) =		x + 1
	2

Wykres tej funkcji przechodzi przez punkty: A = ( 0, 1) i B = ( − 2 , 0) Punkty symetryczne do tych punktów względem O = ( 0, 0 ), to A' = ( 0, − 1) i B' = ( 2 , 0) y = a x + b − 1 = 0*a + b ⇒ b = − 1 0 = 2a − 1 2a = 1

	1
a =
	2

więc wykres funkcji g ma równanie

	1		1
y =		x − 1 ⇒ g(x) =		x − 1
	2		2

=============