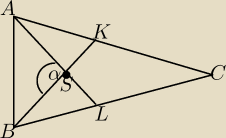
geometria płaska, pole trójkąta, poziom podstawowy ana.: Bardzo proszę o pomoc w zrozumieniu tego zadania. Zaznaczam, ze interesuje mnie tylko podpunkt b) gdyż pierwszy zrobiłam bez większych trudności. Za wszelką pomoc z góry dziękuję Jest to trójkąt równoramienny. Środkowe AL i BK przecinają się w punkcie S pod kątem 60 stopni. Wiadomo, że pole trójkąta ABS jest równe √3. a)Oblicz długość boków trójkąta ABC b)Czy kąt ACB jest równy 30 stopni? Odpowiedź uzasadnij. <proszę o pomoc w tym podpunkcie :3> PS Bardzo bym prosiła o rozwiązanie go metodami na poziomie podstawowym, czyli bez twierdzenia cosinów itd.

PW: Na poziomie podstawowym − znane jest twierdzenie, że kąt wpisany w okręgu ma miarę równą połowie miary kąta środkowego opartego na tym samym łuku. Rozważmy okrąg opisany na tym okręgu.Kąt ACB jest kątem wpisanym. Jeżeli kąt środkowy oparty na tym samym łuku ma miarę 60°, to kąt ACB ma miarę 30°. Czy tak jest w tym trójkącie?

ana.: Jeżeli chodzi o mnie to ja myślałam, ze kąt ACB jest wpisany i ma 30°. Jednakże w odpowiedziach

	3√3
napisane jest iż sin kąta ACB =		, wiec ACB jest < 30°. Wnioskuje zatem, iż jednak
	14

nie jest on kątem wpisanym albo nie rozumiem tego twierdzenia co jest bardzo możliwe.

PW: To może inaczej: umiesz policzyć długości SA, SB i SC?

ana.: SA i SB wyszło mi 2 cm, a a SC 2√3

PW: No i masz odpowiedź: punkt O − środek okręgu opisanego leży na odcinku SC (bo SC jest częścią symetralnej CD − D dorysujemy pośrodku AB). Punkt S nie jest jednak tym środkiem okręgu, bo SA ≠ SC. Skoro S nie jest środkiem okręgu, to kąt ASB nie jest kątem środkowym. AOB ≠ 60°, a więc ACB ≠ 30°.

ana.: Aaaaa... matko takie proste, wielkie dzięki