Płaszczyzna kartezjańska Adrian: Punkty A = (3,1) i B (1,−3) są wierzchołkami trójkąta o polu 3. srodek ciężkości trójkąta nalezy do osi x. Oblicz współrzędne trzeciego wierzchołka trójkąta.

Adrian: ?

Adrian: ?

Eta:

	aA+xB+xC		yA+yB+yC
Środek ciężkości S(		,		)
	3		3

	1−3+yC
S∊ OX ⇒ S(x,0) to yS=		=0 ⇒ yC=2 to C(x, 2)
	3

|AB|=√2²+4²=2√5

	3√5
P(ABC)=3 ⇒ 0,5*|AB|*h=3 ⇒ h=
	5

oraz h =d , gdzie d −−odległość punktu C od prostej AB

	yB−yA
równanie prostej AB: y=		(x−xA)+yA
	xB−xA

to: AB: 2x−y−5=0

	|2x−2−5|		3√5
h=d=		=		⇒ |2x−7|=3 ⇒ ........... x=5 v x= 2
	√5		5

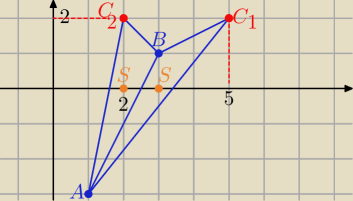
Odp: C₁(5,2) , C₂(2,2)

Eta: ?

bezendu:

Eta:

Adrian: Dziękuję

Eta: