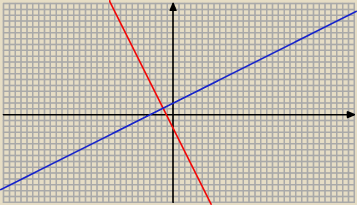
hmmmmmm ehhik: mam znaleźć na osi OY punkt równoodległy od dwóch prostych: k: 6x+3y+7=0 l: x−2y+4=0 z przyrownania odległości P(0,y) od prostej wychodzi:

|3y+7|		|−2y+4|
	=
√45		√5

chciałem to rozwiązać na dwóch przedziałach: y<0 oraz y≥0, ale wynik wychodzi taki sam dla obu.

	5		19
jest poprawny, ale w odpowiedzi są dwa wyniki:		i		. wychodzi mi tylko ten
	9		3

drugi. pewno coś nawaliłem z przedziałami, mam to rozwiązać jak zwykłe równanie z wartością bezwzględną i rozpatrzyć w trzech przedziałach?

ehhik: w sumie to nawet rozpatrując w trzech przedziałach dostaję tylko tę jedną odpowiedź...

Janek191::: P = ( 0, y)

I 3 y + 7 I		I − 2 y + 4I
	=		/ * √45
√45		√5

I 3 y + 7 I = I − 6 y + 12 I I 3 y + 7 I = − 6y + 12 lub I 3 y + 7 I = 6y − 12 1) 3y + 7 = − 6 y+ 12 lub − 3 y − 7 = − 6 y + 12 9y = 5 lub 3 y = 19

	5		19
y =		lub y =
	9		3

=========================== 2) 3 y + 7 = 6 y − 12 lub − 3y − 7 = 6y − 12 3y = 19 lub 9 y = 5

	19		5
y =		lub y =		− to samo, co wyżej
	3		9

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Odp.

	5		19
P1 = ( 0,		) , P2 = ( 0,		)
	9		3

================================

ehhik: ∑

ehhik: dzięki