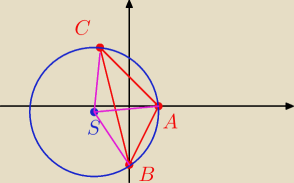
Geometria analityczna Andrzej: Punkty A(1;0),B(0;−2),C(−1:2) są wierzchołkami trójkąta na którym opisano okrąg Wyrazić stosunkiem liczb całkowitych stosunek pól trójkącików na jakie podzielą trójkąt ABC promienie danego okręgu,łączące jego środek z punktami A,B,C

MQ: Będą to sinusy kątów, na jakie podzielą te promienie kąt pełny.

Andrzej: ? ?

Janek191:: ( x − a)² + ( y − b)² = r² ( x − 1)² + y² = r² x² + ( y + 2)² = r² ( x + 1)² + ( y − 2)² = 0 −−−−−−−−−−−−−−−−−−− 1) x² − 2 x + 1 + y² = r² 2) x² + y² + 4 y + 4 = r² 3) x² + 2 x + 1 + y² − 4 y + 4 = r² −−−−−−−−−−−−−−−−−−−−−−− 1) − 2) − 2x + 1 − 4y − 4 = 0 1) − 3) − 4 x + 4 y − 4 = 0 / : 4 ⇒ ( − x + y − 1 = 0) ⇒ y = x + 1 −−−−−−−−−−− − 6 x − 7 = 0 − 6 x = 7

	7
x = −
	6

=========

	7		1
y = −		+ 1 = −
	6		6

===================

	7		1		169		170
r2 = ( x − 1)2 + y2 = ( −		− 1)2 + (−		)2 =		+ U{1}[36} =
	6		6		36		36

więc

	7		1		170
S = ( −		, −		) r2 =
	6		6		36

Janek191:: Dalej : obliczyć długości : I AB I i I AC I i z tw. cosinusów: cos α i cos β α = I ∡ ASC I β = I ∡ BSA I dalej P₁ = 0,5 r² sin α P₂ = 0,5 r² sin β zatem

P1		sin α
	=
P2		sin β

Janek191::

	13		84
cos α =		⇒ sin α =
	85		85

	8		15
cos β =		⇒ sin β=
	17		17

więc

P1		84		15		84
	=		:		=
P2		85		17		75

Janek191:: Policzyłem stosunek innych trójkącików. Trzeba się jeszcze zastanowić nad tym zadaniem

o rany julek: Jasiu,nie podzielisz takiego trójkąta na trzy małe trójkąciki no bo jak, skoro jest on rozwartokątny,co doskonale widać na Twoim rysunku! Można to także potwierdzić rachunkiem: → → → → AB(1−0;0+2),AC(1+1:0−2),AB o AC = 2−4=−2<0 Z tym że Jasiu,nie przejmuj się chwilowym niepowodzeniem i spróbuj wykonać to samo zadanie z trójkątem o wierzchołkach; A(−4:−2),B(3;−1),C(−1;7)