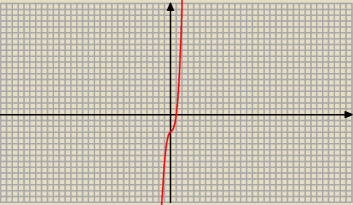
 3 x3 − x2 + x − 3 < 0
3 x3 − x2 + x − 3 ) : ( x − 1) = 3 x2 + 2 x + 3
−3x3 + 3 x2
−−−−−−−−−−
2 x2 + x
− 2 x2 + 2 x
−−−−−−−−−−−−
3 x − 3
− 3 x + 3
−−−−−−−−−−
0
więc mamy
( x − 1)*( 3 x2 + 2 x + 3) < 0
Δ = 4 − 4*3*3 < 0 więc ( 3 x2 + 2 x + 3 ) > 0
x − 1 < 0
x < 1
=====
3 x3 − x2 + x − 3 < 0
3 x3 − x2 + x − 3 ) : ( x − 1) = 3 x2 + 2 x + 3
−3x3 + 3 x2
−−−−−−−−−−
2 x2 + x
− 2 x2 + 2 x
−−−−−−−−−−−−
3 x − 3
− 3 x + 3
−−−−−−−−−−
0
więc mamy
( x − 1)*( 3 x2 + 2 x + 3) < 0
Δ = 4 − 4*3*3 < 0 więc ( 3 x2 + 2 x + 3 ) > 0
x − 1 < 0
x < 1
=====