Wyznacz zbiór wszystkich wartości parametru k rogal: Wyznacz zbiór wszystkich wartości parametru k Dana jest funkcja f(x)=x²−kx−2k² . Wyznacz zbiór wszystkich wartości parametru k , dla których funkcja ma dwa różne miejsca zerowe mniejsze od 6 . Zupełnie nie wiem jak w to zadanie się wgryzć

Eta: Pomagam rysuję ...... chwilkę potrwa....

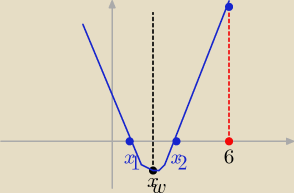Eta: Parabola zwrócona ramionami do góry 1/warunek : Δ>0 −−− bo dwa miejsca zerowe różne 2/ obydwa miejsca < 6 czyli x_w musi leżeć na lewo od 6 => ^−b_2a <6 3/ i f(6) >0 by drugie miejsce zerowe też było < 6 wyznaczając cz. wspólną tych trzech warunków otrzymasz odp do tego zadania. Δ= k² +8k² = 9k² >0 dla k€R \ {0} x_w= ^k₂ <6 => k <12 i f(6)= 36 −6k −6k² >0 => k² +3k −18 <0 Δ₁= 81 √Δ₁= 9 k₁= 3 v k₂= −6 to: k€ (−6,3) wybierając cz. wspólną otrzymamy: odp: k€{−6,0)U(0,3)

rogal: skomplikowane to jest zadanie , skąd wzięło się tam k²+8k²=9k² ?

Eta: Jakie skomplikowane? Najprostszy sposób podałam . A umiesz liczyć deltę? Δ= (−k)² −4*1*(−2k²) = k² +8k² = 9k² ......... jasne? już

Bogdan: Jeśli x₁, x₂ trójmianu kwadratowego jest mniejsze od liczby q (tu q = 6), to przyjmujemy założenia: 1. a ≠ 0 2. Δ > 0 3. a*f(q) > 0

	b		b
4. −		< q gdzie −		= xw, to odcięta wierzchołka paraboli
	2a		2a

Onnar: pozdro

123: A jakbym zrobiłem założenia x₁ i x₂ <6 to dobrzy by wyszło?

Mosiu: tak i nawet nie trzeba wtedy liczyć f(6), więc jest o wiele szybciej, tylko należy pamiętać o tym, by wyrzucić z końcowego przedziału {0}