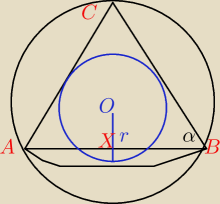
 Tworząca stożka nachylona jest do podstawy pod kątem 45*. Oblicz stosunek objętości kuli
wpisanej w ten stożek do objętości kuli opisanej na tym stożku.
Trójką ABC jest zatem prostokątny równoramienny. Na tym kończy mi się pomysł jak rozwiązać
problem gdy kula jest wpisana w stożek. Wiem, że trzeba pewnie wykorzystać to, że |BX| = |XC|
= a
oraz |CB| = a√2. Ale nie mam pojęcia jak.
Tworząca stożka nachylona jest do podstawy pod kątem 45*. Oblicz stosunek objętości kuli
wpisanej w ten stożek do objętości kuli opisanej na tym stożku.
Trójką ABC jest zatem prostokątny równoramienny. Na tym kończy mi się pomysł jak rozwiązać
problem gdy kula jest wpisana w stożek. Wiem, że trzeba pewnie wykorzystać to, że |BX| = |XC|
= a
oraz |CB| = a√2. Ale nie mam pojęcia jak.
| a√2 | ||
x2 = (a−x)2+( | )2 > tu moje pytanie: czy promień poprowadzony do boku CB dzielo | |
| 2 |
| 4 | ||
a= | x | |
| 3 |
| 4 | 1 | ||
x−x= | x = r | ||
| 3 | 3 |
| 1 | 1 | |||
wynika z tego że r = | h = | a | ||
| 4 | 4 |
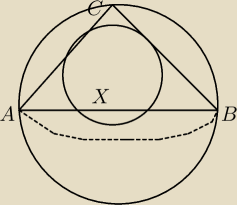 Wiem, wiem. Myślałem że jeśli oznaczę odcinek AX jako a to będę mógł uzależnić od tej wielkości
promienie okręgów wpisanego i opisanego, a potem wszystko się skróci. Rozumiem, że w takim
wypadku R=a. Co jednak z okręgiem wpisanym?
Wiem, wiem. Myślałem że jeśli oznaczę odcinek AX jako a to będę mógł uzależnić od tej wielkości
promienie okręgów wpisanego i opisanego, a potem wszystko się skróci. Rozumiem, że w takim
wypadku R=a. Co jednak z okręgiem wpisanym?
| 1 | 1 | |||
r = | h = | R | ||
| 3 | 3 |