:o
Gabcia : W równoległoboku ABCD dane są wierzchołki A(2,4) B(6,3) C(4,−1) Oblicz
a)pole tego równoległoboku
b)współrzędne wierzchołka D
c)miarę kota α utworzonego przez wektory AK i AL gdzie−K środek boku BC, L− środek boku CD
Tak więc D wyszło mi dobrze że wynosi (0,0)
Wydaje mi się że jest romb czyli także Pole obliczałam ze wzoru 1/2*|AC|*|BC| no i ma wyjść 18
*−*
Nie wiem co robie nie tak, pewnie wszystko ciagle mi wychodzi źle
11 mar 18:54
Gabcia : SOS

11 mar 19:02
Gabcia : SOS

11 mar 19:02
Gabcia : Proszę ładnie o pomoc
11 mar 19:19
Janek191::
a)
→
AB = [ 6 − 2, 3 − 4] = [ 4, − 1]
to
→
BA = [ − 4, 1 ]
→
BC = [ 4 − 6, − 1 − 3 ] = [ − 2, − 4]
więc pole równoległoboku
→ →
P = I det ( BA, BC ) I = I ( − 4)*(− 4) − 1*(−2) I = I 16 + 2 I = 18
b)
→
AB = [ 4, − 1] , D = ( x, y)
→
DC = [ 4 − x, − 1 − y ]
Musi być
→ →
AB = DC
[ 4 , − 1 ] = [ 4 − x, − 1 − y ]
4 = 4 − x i − 1 = − 1 − y
x = 0 i y = 0
D = ( 0, 0)
========
11 mar 19:21
Gabcia : co to za wzór na pole ? co oznacza det?
11 mar 19:31
Gabcia : co to za wzór na pole ? co oznacza det?
11 mar 19:31
Gabcia : 
11 mar 19:37
Gabcia : 
11 mar 19:38
Janek191::
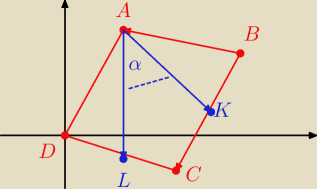
c)
| | 6+4 | |
K = ( |
| , U{3 − 1}{2]) = ( 5, 1) |
| | 2 | |
| | 4 + 0 | | − 1 + 0 | |
L = ( |
| , |
| ) = ( 2; − 0,5) |
| | 2 | | 2 | |
→
AK = [ 5 − 2, 1 − 4] = [ 3, − 3 ]
→
AL = [ 2 − 2, −0,5 − 4] = [ 0 ; − 4,5 ]
Iloczyn skalarny
→ →
AK o AL = 3*0 + (−3)*( − 4,5) = 13,5
Długości wektorów
I AK I =
√32 + (−3)2 =
√9*2 = 3
√2
I AL I = 4,5
więc
| | 13,5 | | 1 | | √2 | |
cos α = |
| = |
| = |
| |
| | 3√2* 4,5 | | √2 | | 2 | |
α = 45
o
==========
11 mar 19:40
Janek191::

c)
| | 6+4 | |
K = ( |
| , U{3 − 1}{2]) = ( 5, 1) |
| | 2 | |
| | 4 + 0 | | − 1 + 0 | |
L = ( |
| , |
| ) = ( 2; − 0,5) |
| | 2 | | 2 | |
→
AK = [ 5 − 2, 1 − 4] = [ 3, − 3 ]
→
AL = [ 2 − 2, −0,5 − 4] = [ 0 ; − 4,5 ]
Iloczyn skalarny
→ →
AK o AL = 3*0 + (−3)*( − 4,5) = 13,5
Długości wektorów
I AK I =
√32 + (−3)2 =
√9*2 = 3
√2
I AL I = 4,5
więc
| | 13,5 | | 1 | | √2 | |
cos α = |
| = |
| = |
| |
| | 3√2* 4,5 | | √2 | | 2 | |
α = 45
o
==========
11 mar 19:40
Janek191::

c)
| | 6+4 | |
K = ( |
| , U{3 − 1}{2]) = ( 5, 1) |
| | 2 | |
| | 4 + 0 | | − 1 + 0 | |
L = ( |
| , |
| ) = ( 2; − 0,5) |
| | 2 | | 2 | |
→
AK = [ 5 − 2, 1 − 4] = [ 3, − 3 ]
→
AL = [ 2 − 2, −0,5 − 4] = [ 0 ; − 4,5 ]
Iloczyn skalarny
→ →
AK o AL = 3*0 + (−3)*( − 4,5) = 13,5
Długości wektorów
I AK I =
√32 + (−3)2 =
√9*2 = 3
√2
I AL I = 4,5
więc
| | 13,5 | | 1 | | √2 | |
cos α = |
| = |
| = |
| |
| | 3√2* 4,5 | | √2 | | 2 | |
α = 45
o
==========
11 mar 19:40
Janek191::
det − wyznacznik pary wektorów

Niech
→
v = [ a , b]
→
w = [ c , d]
to
→ →
det ( v , w ) = a*d − b*c
11 mar 19:43
Gabcia : dzięki wielkie


11 mar 19:49




 c)
c)
 c)
c)
 c)
c)
 Niech
→
v = [ a , b]
→
w = [ c , d]
to
→ →
det ( v , w ) = a*d − b*c
Niech
→
v = [ a , b]
→
w = [ c , d]
to
→ →
det ( v , w ) = a*d − b*c

