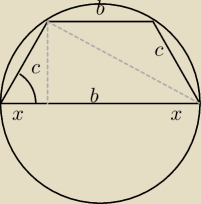
planimetria Michał: Witam, Mam problem z zadaniem. Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.

2x+2b+2c		3
	=
2x+2b		2

	x+b
c=
	2

c		b+2x
	=
x		c

(b+x)²=4bx+4x² b²−2bx−7x²=0 Δ=4x²+28x²=32x² √Δ=4x√2 b=x+2x√2 − drugie rozwiązanie ujemne

	c		(1+√2)x
cosα=		=		=1+√2
	x		x

Tak to robię. W odpowiedziach wynik bardzo podobny, bo √2−1 , ale to jednak spora różnica. Proszę pomóżcie!

Michał: właściwie ten mój cosinus jest do niczego, bo jest większy niż jeden. przez chwilę przypuszczałem, że może błąd w odpowiedziach, ale chyba nie tym razem ...

Michał:

	x		c
no tak, godzinę szukam błędu, a tu się okazuje, że cosα=		, a nie		.... jestem
	c		x

głupi! wychodzi, to forum jest magiczne, zawsze kiedy wejdę i wpiszę zadanie z zeszytu to dostrzegę błąd mimo, że szukałem go godzinę i robiłem 5 razy od nowa...

Tadeusz: (b+x)²=4bx+8x2

Michał: ale potem dobrze wpisałem, literówka