kulka
kyrtap: Qulka?
10 mar 21:56
Qulka: niom
10 mar 21:57
kyrtap: jesteś gotowa na całki niezorientowane ?
10 mar 21:58
kyrtap: bo mam 10 zadań przy czym nie wszystkie rozumiem
10 mar 21:59
Qulka: dawaj
kiedyś się trzeba nauczyć
10 mar 21:59
Qulka: a Krysicki znów został w autku
10 mar 21:59
kyrtap: z Krysickiego nic nie rozumiem, a Skoczylasa przeczytałem ale w niektórych zadaniach jakoś nie
mogę powiązać zagadnień niektórych
10 mar 22:00
kyrtap: Obliczyć moment bezwładności jednorodnego okręgu o promieniu R i masie M względem średnicy.
10 mar 22:01
kyrtap: w zasadzie jakby po fizycznemu liczyć to iloczyn wektorowy siły i promienia
10 mar 22:14
Qulka: wrzućmy go w środek układu współrzędnych x2+y2=r2
gęstość liniowa λ=M/2πR
no to I=2λ∫y2dL
dL = √1+(dy/dx)2 dx
10 mar 22:20
kyrtap: skąd to wytrzasnęłaś I = 2λ∫y
2dL
10 mar 22:22
Qulka: całka w granicach od −R do R
wynik to MR2/2
10 mar 22:24
Qulka: 2 bo dół i góra a całka liczy tylko górę
w fizyce I=mr2 tu r to odległości od osi obrotu (czyli osi x) i są to kolejne współrzędne y i
m trzeba podzielić na kawałki więc masz jak gdyby gęstość liniową λ i to jest stałe więc
wyciągasz przed całkę
10 mar 22:27
Qulka:
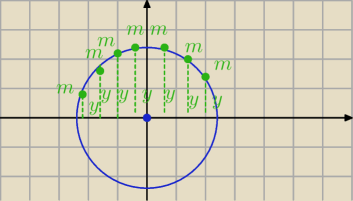
∑my
2
10 mar 22:29
kyrtap: kurde jakie to dziwne
10 mar 22:29
Qulka: coo
10 mar 22:30
kyrtap: nie wiem bo tutaj jest napisane w skoczylasie że moment bezwładności się liczy
Ix = ∫(y2 + z2)λ(x,y,z)dl
i odpowiednio tak dla Iy i Iz
i jeszcze jeden wzór mam taki:
IO = ∫(x2 + y2 + z2) λ(x,y,z)dl
10 mar 22:33
Qulka: definicja momentu bezwładności
że I =∑ m
ir
i2 czyli jak mierzymy w górę I = ∑m
iy
i2
10 mar 22:34
Qulka: a który to Skoczylas?
10 mar 22:35
kyrtap: no tak Qulka mam napisane
10 mar 22:35
kyrtap: taka zielona
10 mar 22:35
Hajtowy: Będę mógł liczyć na pomoc z całkami? Ale to nie dziś
za jakiś czas ^^ Zaczynam z tym
przygodę
10 mar 22:37
Qulka: i tak mam tylko czarnobiałe ksero od kogoś w spadku więc nie wiem ;> a on popełnił chyba 15
książek
10 mar 22:37
kyrtap: mogę ci zdjecie wysłać czekaj Qulka
10 mar 22:38
Qulka: Hajtowy zawsze ktoś pomoże
10 mar 22:40
10 mar 22:42
Qulka: i się zgadza..u nas jest płasko i z=0 więc y
2+z
2 = y
2+0=y
2
i nasz jest jednorodny więc λ jest stałe
10 mar 22:45
kyrtap: jak jest jednorodny to lambda traktować jako stałą?
10 mar 22:52
bezendu:
kyrtap wiedzę mamy to samo
10 mar 22:57
kyrtap: Patryk jest za głupi na studia
10 mar 22:57
Qulka: tak
10 mar 23:04
Qulka: tzn..tak jako stałą
a na studia się po prostu trzeba wdrożyć i przyzwyczaić
10 mar 23:05
kyrtap: spoko Qulka
10 mar 23:06
kyrtap: kolejne mogę podać?
10 mar 23:13
Qulka: dawaj jeśli do tamtego nie masz pytań
10 mar 23:15
kyrtap: nie mam
fajnie to mi wytłumaczyłaś
10 mar 23:15
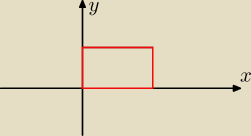
kyrtap: Obliczyć całkę krzywoliniową niezorientowaną ∫xyds gdzie L jest obwodem prostokąta utworzonego
przez proste x = 0, y = 0, x = 4, y = 2
10 mar 23:16
kyrtap:
10 mar 23:19
kyrtap: czyli ds będzie równe 4 + 8 = 12
10 mar 23:22
kyrtap: i to będzie całka oznaczona od 0 do 4 tak?
10 mar 23:33
Qulka: całka tak od 0 do 4 po x i od 0 do 2 po y ale się zastanawiam czy jej się nie rozbija na 2
10 mar 23:34
kyrtap: ja to nawet nie wiem
10 mar 23:37
kyrtap: mam takiego dziadka starego że on nic nie tłumaczy tylko herbatę piję z termosu
10 mar 23:37
Qulka: wszędzie są jakieś funkcje i te różniczki to wiadomo..a jak jest stała to co
mam wyzerować
10 mar 23:39
kyrtap: a może to sparametryzować czy nie?
10 mar 23:41
Qulka: ale to są stałe
to co chcesz parametryzować
10 mar 23:42
kyrtap: Qulka nie smuć się, jestem wdzięczny że chcesz mi pomóc
10 mar 23:42
Qulka: ooooooooooooooooo miałam 2 tom krysckiego i zostawiłam w pracy kiedyś koleżance
tam chyba
to było
10 mar 23:43
kyrtap: właśnie nie wiem
ale nie podoba mi się w tej całe ten x * y
10 mar 23:43
kyrtap: dobra jak nie wiesz to lecimy dalej co?
10 mar 23:49
kyrtap: bo nie ma co się rozwodzić tyle
10 mar 23:49
Qulka: prawie znalazłam
jednak w 2 krysickim to jest
tylko muszę dopasować
10 mar 23:51
kyrtap: w takim razie czekam a ja zrobię to 1 zadanie
i spiszę je do zeszyciku
10 mar 23:53
11 mar 00:00
kyrtap: a może to tak ma być że stałe ?
11 mar 00:01
11 mar 00:03
kyrtap: Twierdzenie to będę miał dopiero
11 mar 00:04
Qulka: no to podziel ją na 4 kawałki i policz każdą oddzielnie
11 mar 00:08
kyrtap: dobra z tym zadaniem się przejdę na konsultacje
wracając do pierwszego
dL =
√1+(dy/dx)2 dx
takie coś napisałaś
dy/dx
mam liczyć
z równania okręgu?
11 mar 00:10
kyrtap: wyznaczając y tak?
11 mar 00:10
Qulka: tak
11 mar 00:12
kyrtap: dobra czyli 1 odhaczam że umiem
a drugie na konsultacje
11 mar 00:13
Qulka: nie masz odpowiedzi?
11 mar 00:15
kyrtap: | | 1 | |
3. Obliczyć ∫ |
| ds L: odcinek łączący punkty A =(0,−2) , B= (4,0) |
| | x−y | |
czyli tutaj najlepiej sparametryzować odcinek, policzyć ds jako
√(x'(t)2 + (y'(t))2 i potem
policzyć całkę oznaczoną od 1 do 0 tak?
11 mar 00:16
kyrtap: nie własnie
11 mar 00:16
Qulka: bo mi wyszło 24
11 mar 00:16
kyrtap: mogłabyś pokazać w jaki sposób liczyłaś i spr 3 czy dobrze myślę
11 mar 00:17
Qulka:
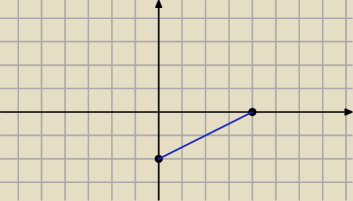
albo jawnie y=x/2−2 i x od 0 do 4
11 mar 00:17
kyrtap: y = x/2−2
11 mar 00:19
Qulka: podzieliłam na 4 całki
∫xydx +∫xydy+∫xydx +∫xydy = yx2/2 +xy2/2 − yx2/2 − xy2/2 (minus bo w drugą stronę
2•42/2+4•22/2−0•42/2 −0•22/2
11 mar 00:21
Qulka: i wyszło 24
11 mar 00:22
kyrtap: a ty mówisz o 2
11 mar 00:22
Qulka:
ten odcinek to kawałek prostej o takim równaniu
11 mar 00:22
kyrtap: ale parametryzacja nie jest zła?
11 mar 00:24
Qulka: chwilami o drugim chwilami o 3
11 mar 00:24
Qulka: nie jest zła..bo wszystkie wzory mają t
11 mar 00:24
kyrtap: dobra kolejne zadanie
Obliczyć masę krzywej y = lnx e≤x≤e
2 jeżeli liniowa gęstość masy w punkcie jest równa
kwadratowi odciętej tego punktu
11 mar 00:26
kyrtap: czyli w tym wypadku M = ∫λ(x,y) dl mam granice całkowania bo to bedzie od e do e2 oraz wiem
jak policzyć dl ale co tutaj z gęstością?
11 mar 00:28
Qulka: λ=x2
11 mar 00:30
kyrtap: dobra nie było pytania
11 mar 00:31
Qulka: ja poproszę tylko takie
11 mar 00:31
kyrtap: to Qulka to jeszcze jedno i daje spokój co?
11 mar 00:31
kyrtap: przerobiliśmy tym sposobem już 5 zadań
11 mar 00:32
kyrtap: z 10
11 mar 00:32
kyrtap: albo chyba umiem resztę
11 mar 00:39
kyrtap: dzięki śliczne
11 mar 00:39
Qulka: dawaj
tyle wiemy o sobie na ile nas sprawdzono
11 mar 00:40
Qulka: chyba że umiesz
11 mar 00:40
Qulka: to jest nadzieja że i ja dziś pójdę wcześniej spać
11 mar 00:41
kyrtap: no nadzieja jest
11 mar 00:53
kyrtap: jak coś to jeszcze jutro się odezwę na pewno
11 mar 00:53
Qulka: zapraszam
douczyć się nie zdołam, ale może uda mi sie poszukać jeszcze jakoś notatek
11 mar 00:54
kyrtap: i tak dużo wiesz a ja w czwartek się przejdę jeszcze na konsultacje do innego profesora,
powinien też mi coś pomóc
11 mar 01:01
Qulka: kiedyś umiałam więcej
ale jak niepotrzebne było to się neurościeżki zagubiły
11 mar 01:03
kyrtap: i tak dużo wiesz w przeciwieństwie do mnie
11 mar 01:04
kyrtap: | | M | |
Qulka z tego |
| ∫√R2− x2dx od R do −R jeśli chodzi o zadanie 1 wyjdzie to co |
| | π | |
napisałaś?
11 mar 01:33
kyrtap: taka całka mi wyszła i nie wiem czy dalej ją liczyć
11 mar 01:34
Qulka: chyba mało masz
11 mar 01:51
Qulka: oki..licz dalej
11 mar 01:56
kyrtap: wyszło mi 2M
11 mar 11:22
kyrtap: ale niby według twojej metody poprawnie wyliczyłem więc może tak będzie
11 mar 11:34
Qulka: musi zależeć od R gdzieś masz źle
11 mar 12:12
kyrtap: a do tego momentu mam dobrze co napisałem
11 mar 12:16
Qulka: tak tamto było OK
11 mar 12:24
kyrtap: | | 1 | |
no to chyba dobrze policzyłem całkę ∫√R2 −x2 dx bo wyszło mi z niej |
| x√R2− x2 + |
| | 2 | |
11 mar 12:27
Qulka: przed arc R2/2
11 mar 12:42
kyrtap: dobra widzę błąd
11 mar 15:21
Qulka: bo właśnie wychodzę i już się bałam że jestem potrzebna
11 mar 15:22
kyrtap: o której będziesz dostępna na forum?
11 mar 15:24
Qulka: pewnie po 22 tradycyjnie
11 mar 15:29
kyrtap: ok
11 mar 15:34