funkcja kwadratowa uliczny druid: Witam prosiłbym o pomoc w rozwiazaniu kilku zadan,nie chce całych rozwiazan,ale wskazówki i kroki jak to zrobic

	x+5
1.Zbiorem wartosci funkcji f(x) =		− Ułamek{√ 4x2 −8x + 4
	√x2+10x+25

mianownik{2x−2} jest zbiór ? 2.Dane sa funkcje f(x) = 2x² − 8x + 1 i g(x) m²x² + (4m+1)x+3 gdzie m jest roznce od 0.Funkcja g osiaga ekstemum lokalne w tym samym punkcie co funkcja f gdy ? z gory dziekuje i prosze o pomoc

Qulka: wzory skróconego mnożenia masz pod tymi pierwiastkami

uliczny druid:

	x+5		|2x−2|
No i wyszło mi		−		i teraz jak to uporzadkowac czy jak to teraz
	|x+5|		2x−2

wyznaczyc

uliczny druid: 2x² + 8x−10 − | 2x²+12x−10 | mianownik |x+5|(2x−2)

pigor: ..,

	|x+5|		|x−1|
f(x)=		−		i xR\{−5,1} , to teraz rozpisuj
	|x+5|		x−1

i skracaj w 3−ech przedziałach : x< −5 v −5< x< 1 v x>1, to zobaczysz swoje szukane wartości funkcji f . .....

pigor: ...

uliczny druid: mógłbym prosic o pomoc w tego rozwiazaniu ? jednak pojawił sie problemy jak to zrobic dalej

uliczny druid: wiem ze ma wyjsc przedizał { 0;2 }

Qulka:

uliczny druid: Tak,ale chciałbym sie nauczyc rozwiazywac takie cos

Qulka:

|a|
	=
a

1 gdy a>0 bo |a|=a lub −1 gdy a <0 bo |a|=−a

uliczny druid: Nie rozumiem jak sie to ma tutaj do tego,wiem że zapisałeś/zapisałaś warunki wartości bezwzględnej,konkretnie na tym przykładzie bym poprosił

Qulka: zastąp sobie 'a' np x+5

|a|
	= 1 lub −1 bo j.w
a

uliczny druid: naprawde nie wychodzi mi to,prosze o pomoc

uliczny druid: 2.Dane sa funkcje f(x) = 2x2 − 8x + 1 i g(x) m2x2 + (4m+1)x+3 gdzie m jest roznce od 0.Funkcja g osiaga ekstemum lokalne w tym samym punkcie co funkcja f gdy ?

Janek191:: f(x) = 2 x² − 8 x + 1 g(x) = m² x² + ( 4 m + 1) x + 3, m≠ 0 Ma być p₁ = p₂

	8
p1 =		= 2
	2*2

	− 4 m − 1
p2 =
	2 m2

więc

	− 4 m − 1
2 =
	2 m2

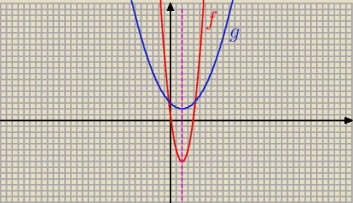
− 4 m − 1 = 4 m² 4 m² + 4 m + 1 = 0 ( 2m + 1)² = 0 2m = − 1 m = − 0,5 ======= Spr. m = − 0,5 g(x) = 0,25 x² − x + 3 Wykresy: