matematykaszkolna.pl
analiza wektorowa kyrtap: Qulka ?
9 mar 22:10
kyrtap: emotka
9 mar 22:30
Qulka: niomemotka
9 mar 22:33
kyrtap: jakbym podesłał jutro kilka zadań odnośnie analizy wektorowej zerknęła byś czy dobrze zrobione?
9 mar 22:39
Qulka: oczywiście że popatrzę emotka czy na 100% będę w stanie przeanalizować to w ciemno nie obiecuję emotka są rzeczy których zapomniałam emotka
9 mar 22:41
kyrtap: głównie to całki zorientowane i niezorientowane
9 mar 22:42
kyrtap: Qulka mam jedno dzisiaj zadanie abyś mi je omówiła, w sensie chodzi mi o tą parametryzację: Napisać parametryzacje łuków dla każdego z kierunków przebiegu tutaj podpunkt: a) część na które prosta x = −4 i dzieli okrąg x2 + 2x + y2 − 4y = 7
9 mar 23:23
kyrtap: bez "i"
9 mar 23:23
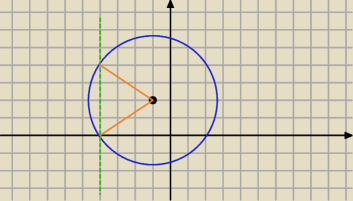
Qulka: rysunek
9 mar 23:31
kyrtap: a skąd wiesz jak policzyć ten kącik? emotka
9 mar 23:39
Qulka: cos α = 3/√12 cały = 2α
9 mar 23:43
kyrtap:
 3 
nie czaję skąd cosα =
?
 √12 
9 mar 23:46
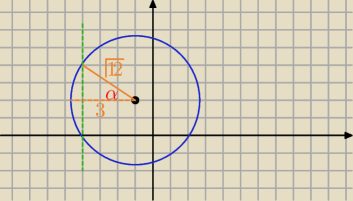
Qulka: rysunekpromień to √12 a od x= −1 do x= −4 jest równo 3
9 mar 23:53
kyrtap: teraz czaję emotka
10 mar 00:11
Qulka: i mam pisać dalej
10 mar 00:31
kyrtap: nie emotka
10 mar 00:36
kyrtap: ale jedno jeszcze zadanie mam emotka
10 mar 00:36
kyrtap: masz siłę jeszcze?
10 mar 00:36
Qulka: dawaj emotka na razie nie wymagały jakieś wielkiej inwencji poza paroma kreskami emotka i kółeczkiem emotka
10 mar 00:37
kyrtap: Obliczyć pole części powierzchni walca parabolicznego y2 = 4(1−x) ograniczonego płaszczyznami x = 0, z = 0 i powierzchnią z = |y|.
10 mar 00:38
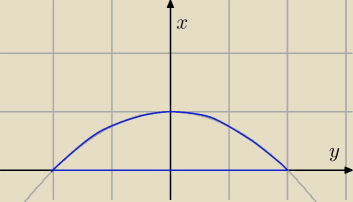
Qulka: rysunek
10 mar 00:47
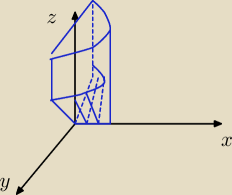
Qulka: rysunek
10 mar 00:51
Qulka: chyba nie będzie widaćemotka
10 mar 00:52
kyrtap: tylko z tego wynika że funkcja jest parzysta
10 mar 00:54
kyrtap: nie wiem co z tym że z = |y|
10 mar 00:54
Qulka: niom..możesz policzyć pół emotka
10 mar 00:54
Qulka: z=|y| to ten płaski szpic..jak rozłożona książka gdzie grzbiet to oś x
10 mar 00:55
Qulka: y2 = 4(1−x)
10 mar 00:57
Qulka: http://www.wolframalpha.com/input/?i=+plot3D+++z%3D%7Cy%7C
10 mar 00:57
kyrtap: hm trochę to dziwne muszę dać jakąś parametryzację ?
10 mar 01:20
Qulka: dziwne jest z=0, a nie obcięli go od góry .. od dołu obcina go moduł
10 mar 01:21
kyrtap: nie wiem jak to zadanie rozwalić
10 mar 01:29
Qulka: myślę nad nim co chwilę.. albo nad tym jak zmusić wolframa by to namalował emotka
10 mar 02:04
Qulka: jednak będzie się na z kończył na 1 http://www.wolframalpha.com/input/?i=+plot++%28+x%3D%281-+t%5E2%2F4%29%2C+y%3Dt+%2C+z%3D%7Ct%7C+%29+from+t%3D-2+to+2
10 mar 02:12
Qulka: a nie to oś x emotka wyobraźnię trzeba mieć bez wersji proemotka
10 mar 02:16
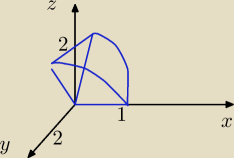
Qulka: rysunek
10 mar 02:18
Qulka: chyba muszę przypomnieć sobie całki wielokrotne
10 mar 02:37