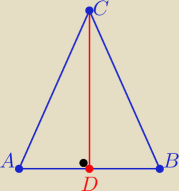
Arkusz maturalny p.r. Dżepetto 18: W trójkącie równoramiennym ABC o podstawie AB wierzchołek C=(3, −3). podstawa trójkąta zawiera się w prostej o równaniu x−y+2=0, a jego pole jest równe 24. Wyznacz współrzędne pozostałych wierzchołków trójkąta ABC. Ew. Wzór na pole trójkąta: [[[http://portalwiedzy.onet.pl/inl/mat_10_28.gif]]]

	1
Z odległości punktu od prostej wyliczę h tego trójkąta. następnie z pitagorasa długość
	2

podstawy AB. Następnie przydałby się punkt podstawy wysokosci poprowadzonej na AB. Lecz mam zaćmienie. Ktoś pomoże

Dżepetto 18: * http://portalwiedzy.onet.pl/inl/mat_10_28.gif

prosta: Można policzyć długość ramienia i zbudować równanie na współrzędne punktu A i B

prosta: A=(x, x+2), C=(3,−3) |AC|=b..... b²=(0,5a)²+h²

prosta: ah=2P

prosta: h − odległość punktu od prostej

Dżepetto 18: ale jak wyliczyć współrzędne A i B mając długość ramion, jak zbudować jakieś równanie? :c

prosta: |AC|=√(x−3)²+(x+2+3)² √(x−3)²+(x+5)²=b pozostanie tylko niewiadoma x (x−3)²+(x+5)²=b ²

Dżepetto 18: Potem wyliczam tylko x podstawiam do A a następnie liczę punkt B po danej prostej w takiej samej odległości jak od podstawy wysokości do A. Wszystko jasne, dziekuję!

prosta: od razu wyjdzie punkt A i B....z tego równanie

prosta: A(x₁,X₁+2) B(X₂, X₂+2)

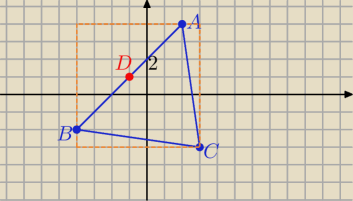
Eta: P= 24 , C(3, −3) AB : y= x+2 ⇒ A(x, x+2) proste AB i DC są prostopadłe to DC : y= −(x−3)−3 ⇒ DC : y= −x DC ∩ AB= D

⎧	y=x+2
⎩	y= −x	⇒ D(−1,1)

→ → P(ABC)=2P(ADC)= |d(AD, DC)| AD=[x+1, x+2−1]= [x+1, x+1] i DC=[4,−4] to: |(x+1)*(−4)−(x+1)*4|=24 ⇒ |x+1|=3 ⇒ x=2 v x= −4 to y=4 v y= −2 A(2, 4) , B(−4, −2)

Eta: Sprawdzenie : P(ABC)= 7²−(18+7)= 24 ok i AB : y=x+2 ok

Dżepetto 18: Dziękuję Eta, wczoraj zrobiłem szkic dziś biorę się za to zadanie. Teraz jest mi jeszcze łatwiej. Dziękuję!

Dżepetto 18:

	1
Eta, jedno pytanie odnośnie Twojego sposobu. Czy pr. prostopadła nie ma równania y= −
	x

+b?

	1
Podstawiłaś do pr. DC punkt D lecz czy wzór prostej nie powinien być taki y= −		−3?
	x−3

Eta: Prawie spadłam z krzesła

	1
y= −		−−−− to równanie hiperboli
	x

Nie pisz więcej takich bzdur