Stożki elcia : Powierzchnia boczna stożka po rozwinięciu jest półkolem . Kąt rozwarcia tego stożka ma miarę? PROSZĘ O WYTŁUMACZENIE.

elcia : ?

elcia : ktos pomoże?

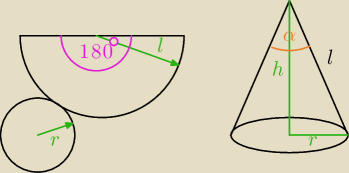
dero2005: rysunek po lewej stronie − rozwinięcie powierzchni bocznej liczymy długość obwodu półkola o promieniu l i porównujemy ją z długością obwodu okręgu o promieniu r (dna)

180
	2πl = 2πr
360

l = 2r rysunek po prawej stronie − prawo cosinusów (2r)² = 2l² − 2l²cosα l² = 2l² − 2l²cosα 2l²cosα = 2l² − l² = l²

	l2		1
cosα =		=
	2l2		2

α = 60^o

elcia : ?

elcia : dero2005: A te l=2r skąd się wzięło?

dero2005: rozpracuj pierwszy wzór

elcia : A ten pierwszy wzór na co on jest? Nie mam go w podręczniku.

dero2005: już tłumaczę: obwód koła o promieniu l ma wzór 2πl

	180
obwód półkola (na rysunku po lewej) o promieniu l ma wzór		*2πl bo półkole ma kąt
	360

180 ^o ten obwód półkola musi pasować do długości obwodu koła podstawy (dna stożka) wzór 2πr jeśli musi pasować to znaczy że ich długość jest taka sama a więc pomiędzy tymi wzorami stawiamy znak równosci

180
	2πl = 2πr
360

1
	2πl = 2πr
2

πl = 2πr l = 2r

dero2005: ¹⁸⁰₃₆₀2πl = 2πr l = 2r

elcia : Ok już rozumiem. teraz liczysz ten mały trójkącik po prawej stronie tak ? A czemu akurat korzystasz z cosinusów ? 2l² skąd to się wzięło?

elcia : z sinusów też chyba można

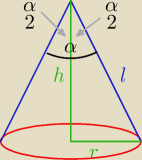
dero2005: to jest jeden z wariantów możesz też obliczyś z funkcji sinus

r		r		1
	= sinα2 =		=
l		2r		2

α
	= 30o
2

α = 60^o

elcia : Ok,rozumiem z sinusów chyba łatwiej wychodzi.

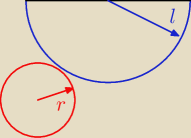
elcia : a te zadanie ` wycinek koła o promieniu 2 wyznaczony przez kąt 90 stopni zwinięto w powierzchnię boczną stożka. oblicz pole powierzchni całkowitej tego stożka.

elcia : 90 −−−−* 2πl = 2πr 360 1 −−− *2πl=2πr 4 tak ?