ANALIZA MATEMATYCZNA PROSZE O POMOC KACPER: BARDZO PROSZE O POMOC W TYCH ZADANIACH. mam do rozwiazania 3 zadania 1. Oblicz ekstrema lokalne i punkty przeciecia funkcji f(x)=x2(5−x) 2.Oblicz pole obszaru ograniczonymi krzywymi y=x(4−x) i x+y=0

	x2−2x+2
3.a) ∫
	√x

bardzo prosze o pomoc, potrzebuje tego na jutrzejsze zaliczenie

ola: Trzeba wcześniej zabierać się do nauki. f(x)=x²*(5−x) 1) D=R 2) miejsca zerowe: x²*(5−x)=0⇔ x²=0 lub 5−x=0 x=0 ( pierwiastek podwójny) lub x=5 3)Ekstrema f(x)=5x²−x³ f'(x)=10x−3x² 10x−3x²=0 ⇔x(10−3x)=0⇔

	10
x=0 lub x=
	3

Badamy znak pochodnej

	10
f'(x)>0 dla x∊(0,		)
	3

dla x=0 f(x) ma minimum f(0)=0

	10
dla x=		funkcja ma maksimum ( pochodna zmienia znak z dodatniego na ujemny)
	3

	10		10		10		100		5		500
f(		)=(		)2*(5−		)=		*		=		=181427
	3		3		3		9		3		27

4) lim_x→−∞[x²*(5−x)]=∞ lim_x→∞[x²*(5−x)]=−∞

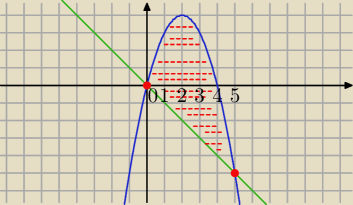ola: 2.Oblicz pole obszaru ograniczonymi krzywymi y=x(4−x) i x+y=0 y=4x−x² y=−x Punkty przecięcia wykresów. −x=4x−x² x²−5x=0 x(x−5) =0 x=0 lub x=5

	1		5
P=0∫5[4x−x2−(−x)]dx=0∫5(−x2+5x) dx=[−		x3+		x2]05=
	3		2

	1		5		125		125		2		3		125
−		*53+		*52−0=−		+		=125*(−		+		)=
	3		2		3		2		6		6		6