Geometria analityczna - potrzebna pomoc!!! Kajak: Witam serdzeczie i proszę o pomoc w zadaniu : Punkty A(−1, −3) i B(−3, −1) leżą na hiperboli o równaniu y = ³_x, gdzie x (różne od) 0. Znajdz na tej hiperboli taki punkt C o dodatniej odciętej, aby pole trójkąta ABC było jak najmniejsze.

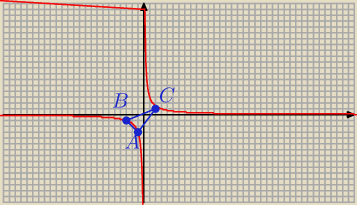
Janek191:: A = ( − 1, − 3) B = ( − 3, − 1)

	3
C = ( x ;		) , x > 0
	x

→

	3
CA = [ − 1 − x , − 3 −		]
	x

→

	3
CB = [ − 3 − x , − 1 −		]
	x

Pole ΔABC → →

	3		3
P = 0,5* I det ( CA, CB ) I = 0,5* I ( − 1 − x)*( − 1 −		−( − 3 − x)*( − 3 −		) I =
	x		x

	3		9		3
= 0,5 I 1 +		+ x + 3 − ( 9 +		+ 3 x + 3 ) I = 4 +		+ x
	x		x		x

	3
P '(x) = −		+ 1 = 0 ⇔ x = √3
	x2

	6
P ''(x) =		oraz P ''( √3) > 0 więc dla x = √3 funkcja P osiąga minimum.
	x3

zatem

	3
dla x = √3 mamy y =		= √3
	√3

C = ( √3, √3 ) =============

pigor: ..., ciekawe co by powiedział egzaminator na takie rozwiązanie : z symetrii osiowej danych zadania względem prostej y= x , z układu równań y=x i y=³_x i x >0 ⇒ x= ³_x ⇒ x²=3 ⇒ ⇒ |x|=√3 i x>0 ⇒ x=√3=y ⇒ C= (x,y) =(√3, √3) . ...

pigor: .... dopisałbym jeszcze np. to przy stałej podstawie pole Δ równoramiennego (z symetrii) najmniejsze, gdy wysokość o wspólnym końcu prostej y=x i hiperboli najkrótsza (najmniejsza) . ..