Igor:

	4
Punkty A(−4,−1) i B(−2,−2) należą do hiperboli o równaniu y=		. Wyznacz współrzędne punktu
	x

C o odciętej dodatniej, należącego do danej hiperboli i takiego, że pole trójkąta ABC jest najmniejsze.

Kam: Jest jakiś łatwiejszy sposób na obliczenie pola trójkąta ABC, nie licząc pola z Herona?

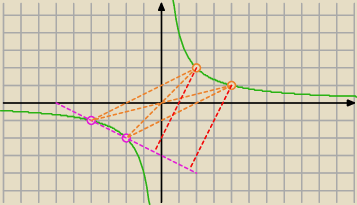
===: Musisz zauważyć, że szukasz punktu należącego do hiperboli (o odciętej dodatniej) a jednocześnie położonego najbliżej prostej przechodzącej przez punkty A i B. Odcinek AB to podstawa trójkąta zaś odległość punktu C od prostej przez A i B to wysokość)

iza: → → P=0,5 |d(AB, AC)|

===: nikt tu o pole tego trójkąta nie pyta

Kam: Dzięki za pomoc.

anubas: Podstawa, tzn. odległość AB jest stała, więc pole zależy tylko od wysokości trójkąta. Wysokość, tak jak ktoś już powiedział, jest odległością punktu C(x,4/x) od prostej AB. Liczymy pochodną odległości i znajdujemy miejsce zerowe. Odpowiedź to zdaje się C(2√2,√2).