Zbiór wartości funkcji wymiernej z wartością bezwzględną criBaroque: Tutaj składam jedynie prośbę o wytłumaczenie pewnego fragmentu rozwiązywania zadania. Jest to temat sprzed prawie roku i odpowiedział w nim Grześ. " Grześ: a ja pokażę sposób algebraiczny bez rysowania wykresów. Jeśli ktoś jest zainteresowany. 2|x|−1 Wyznaczenie zbioru wartości funkcji f(x)= , to ułożyć takie równanie: |x|+1 2|x|−1 =p, które dla p∊R, ma choć jedno rozwiązanie emotka |x|+1 Znajdujemy wartości p: 2|x|−1=p|x|+p (2−p)|x|=p+1 dla p=2 mamy: 0*|x|=3, sprzeczność, czyli brak rozwiązań Teraz dla p≠2, dzielimy przez (2−p) p+1 |x|= 2−p Teraz to równanie ma rozwiązaniem tylko, gdy: p+1 ≥0 p≠2 2−p −(p+1)(p−2)≥0 (p+1)(p−2)≤2 p∊<−1,2) Czyli ZW=<−1,2) Jak ktoś zainteresowany, to sobie to przeanalizuje emotka " Dokładnie mi chodzi o końcowy fragment, tutaj: p+1 ≥0 p≠2 2−p −(p+1)(p−2)≥0 <−−−− ≥0, bo wartość bezwzględna i jedynie wyciągnięcie − przed nawias dla lepszego wyglądu? (p+1)(p−2)≤2 <−−− ? czemu akurat ≤2, a nie <, >, ≥? No i gdzie ten minus z przodu? p∊<−1,2) Jeżeli ktoś takowe posiada, to mógłby podesłać zadania z rozwiązaniem tego samego typu?

criBaroque:

	2|x|−1
f(x)=
	|x|+1

criBaroque: bump

PW: Zbiór wartości funkcji

	2|x| − 1
f(x) =		?
	|x| + 1

	2|x| + 2 −3 1
f(x) =
	|x| + 1

	3
f(x) = 2 −		.
	|x| + 1

Jak widać wystarczy zbadać zbiór wartości funkcji

	3
g(x) =		.
	|x| + 1

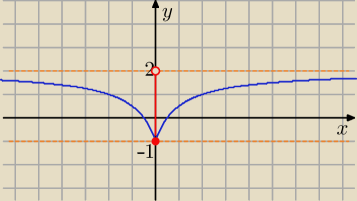
Badanie jest banalne − mianownik jest najmniejszy dla x = 0, wtedy funkcja przyjmuje największą wartość 3. Mianownik nie jest ograniczony z góry, wartości ułamka mogą być dowolnie małe (dodatnie). Funkcja g nie osiąga zatem wartości najmniejszej, wszystkie wartości są dodatnie. Zbiorem wartości funkcji g jest przedział (0, 3], wobec tego − 3 ≤ − g(x) < 0 2 − 3 ≤ 2 − g(x) < 2 −1 ≤ f(x) < 3. Zbiorem wartości funkcji f jest przedział [−1, 2).

PW: Poprawka w przedostatnim wierszu: −1 ≤ f(x) < 2 (wcisnąłem sąsiedni klawisz)

criBaroque: Takiego sposobu rozwiązywania zbioru wartości jeszcze nie widziałem, dziękuję bardzo. Tylko spróbuję jeszcze raz zapytać akurat o tamto rozwiązanie, ten inny sposób. Po prostu chciałbym zrozumieć dokładnie ten dział. Po prostu wkleję link do zdjęcia rozwiązania które tak nieudolnie skopiowałem. http://screenshu.com/static/uploads/temporary/yu/r1/v5/4pmrmf.jpg No i jeszcze raz: fragment, na samym dole.

p+1
	≥0 p ≠2 ← ≥0, bo wartość bezwzględna
2−p

	W(x)
−(p+1)(p−2)≥0 ← bo		≥0 ⇔W(x)Q(x)≥0
	Q(x)

(p+1)(p−2)≤2 ← skąd to? Tylko o wytłumaczenie tego na dole proszę.

criBaroque: Stąd, że wcześniej (od wartości bezwzględnej) x≥0, to teraz x<0? Czemu pojawiła się tutaj w ogóle 2, no i dlaczego znak "≤", nie "<"?

PW:

	2|x| − 1
		= p
	|x| + 1

Mnożymy przez mianownik obie strony rownania: 2|x| − 1 = p(|x| + 1) 2|x| − p|x| = p + 1 |x| (2 − p) = p + 1

	p + 1
(1) |x| =		.
	2 − p

Dla x = 0 mamy p = − 1 − to żadna rewelacja, że wartość funkcji.f dla x = 0 jest równa −1, mogliśmy to obliczyć bezpośrednio − podstawiając x = 0 do wzoru definiującego funkcję. Dla pozostałych x lewa strona (1) jest dodatnia, równanie to można zatem zinterpretować tak: − jeżeli istnieje liczba p będąca rozwiązaniem nierówności

	p + 1
(2)		> 0,
	2 − p

to jest ona wartością funkcji f. Dlatego rozwiązujemy nierówność (2) − w zwykły sposób, na zasadzie "iloraz ma taki sam znak jak iloczyn": − (p+1)(p−2) > 0 (p+1)(p−2) < 0. Rowiązaniami są liczby z przedziału (−1, 2), a o liczbie −1 wcześniej wiedzieliśmy, ze jest wartością funkcji f, stąd odpowiedź [−1, 2). Ta dwójka po prawej stronie nierówności to zwyczajna pomyłka. Dlatego nie lubię sprawdzać cudzych obliczeń, wolałem podać własne − chyba łatwiejsze do zrozumienia. Musisz przyznać, że Grześ nie napisał jasno tego, co zaznaczyłem na niebiesko.

Eta:

Eta:

criBaroque: Doobra, to już wszystkie znane mi sposoby ogarnięte. Dzięki wielkie za poświęcony czas, baaardzo mi to pomogło. ♥