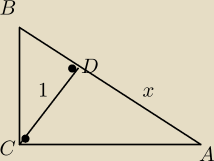
 Wysokość CD opuszczona z wierzchołka C trójkąta prostokątnego ABC na przeciwprostokątną AB ma
długość 1. Zapisz długość tej przeciwprostokątnej jako funkcję zmiennej x, gdzie x=|AD|.
Wyznacz argument, dla którego przeciwprostokątna ta jest najkrótsza i oblicz pole tego
trójkąta.
:(
hmm no nie mam pomysłu
Wysokość CD opuszczona z wierzchołka C trójkąta prostokątnego ABC na przeciwprostokątną AB ma
długość 1. Zapisz długość tej przeciwprostokątnej jako funkcję zmiennej x, gdzie x=|AD|.
Wyznacz argument, dla którego przeciwprostokątna ta jest najkrótsza i oblicz pole tego
trójkąta.
:(
hmm no nie mam pomysłu
 ?
?
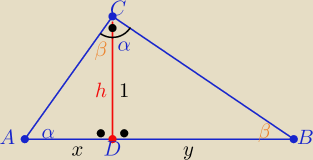 Z podobieństwa trójkątów ADC i DBC
Z podobieństwa trójkątów ADC i DBC
| h | y | ||
= | ⇒ h=xy , x, y >0 | ||
| x | h |
| 1 | ||
to x*y= 1 ⇒ y= | ||
| x |
| 1 | 1 | |||
to c(x)= x+ | , c'(x)= 1− | 2 ⇒ dla x=1 −− osiąga minimum | ||
| x | x |
| 1 | ||
c'(x)= 1− | ||
| x2 |
 Możesz zajrzeć do mojego postu?
Nie wiem czy dobrze stawiam warunki, a jutro kroi mi sie z tego sprawdzian.
Możesz zajrzeć do mojego postu?
Nie wiem czy dobrze stawiam warunki, a jutro kroi mi sie z tego sprawdzian.
 w razie watpliwosci bede
jeszcze pytać
w razie watpliwosci bede
jeszcze pytać
