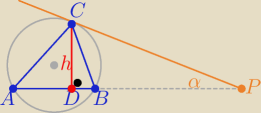
styczne i sieczne prosta: Na trójkącie ABC o polu 8 opisano okrąg. Z punktu P leżącego na półprostej BA poprowadzono styczną do okręgu w punkcie C. Oblicz długości odcinków AB i PB jeśli |PC|=4 oraz sinus kąta APC równa się 2/3

prosta: może jakieś wskazówki...rozwiązałam...potrzebne potwierdzenie

Mila: Z czym tu masz problem?

Eta: |AB|=6 , |PB|=2 , |AP|=8

prosta: napiszę jak rozwiązałam: AB|=a, |PB|=x z tw. o stycznej i siecznej: x(x+a)=42 z wzoru na pole trójkąta: 2P_PBC=2P_PAC+2P_ABC 4(x+a)sinα=4xsinα+16 4asinα=16 a=6 x(x+a)=16 ⇒ x=2

prosta: dzięki

prosta: można liczyć jakoś inaczej?

prosta: powinno być: x(x+a)=4²

Eta:

	|DC|		2		8
|CP|=4 i		=		⇒ |DC|=
	|CP		3		3

	|DC|*|AB|
P(ABC)=		=8 ⇒ |AB|*|DC|=16 ⇒ |AB|=6
	2

Z tw. o siecznej i stycznej |CP|²|AP|*|BP|= 16 ⇒ (x+6)*x=16 ⇒ x=2 .............

pigor: ..., zamiast sumy pól stosunek pól ΔΔ o jednakowych wysokościach np. taki

PΔPBC		x
	=		⇒ a*12x*4*23 = 8x ⇔ a=2*3=6= |AB|
PΔABC		a

prosta: Dziękuję