Romb
Kripp: W romb można wpisać okrąg. Podaj długości przekątnych tego rombu wiedząc że jego wysokość
wynosi 2,4 cm.
8 mar 17:05
Kripp: Niech ktoś to zrobi boyz.
8 mar 17:19
Kripp: Pomoże ktoś
8 mar 19:52
Mila:
W każdy romb można wpisać okrąg.
h=2r
Za mało danych, aby obliczyć przekątne.
8 mar 20:33
Mila:
Może to zadanie zamknięte?
8 mar 20:34
Hektor: tak jest zamknięte a Odpowiedzi To:
6 , 7 , 8 , 9
8 mar 20:40
Mila:
Podaj dokładną treść zadania, bo przekątne są dwie, więc powinny być 4 pary.
8 mar 20:45
Hektor: Pytają o sumę długości tych przekątnych, no ale myślałem że i tak trzeba je policzyć.
8 mar 20:47
Hektor: Dasz radę?
8 mar 21:12
Mila:
W tej chwili nie mam prostego sposobu. Myślę.
7
To zadanie z Rozszerzonego poziomu?
8 mar 21:42
Eta:
Nie
improwizuj tylko napisz poprawną treść zadania!
W
każdy romb można wpisać okrąg
więc zadanie nie może zaczynać się : "w romb można wpisać okrąg"
Znalazłam zadanie takiej treści:
W romb o boku długości 2,5 wpisano okrąg
Wysokość rombu ma długość 2,4. Oblicz sumę przekątnych tego rombu
| | e*f | |
h=2,4 , a=2,5 to P=a*h= 6 i P= |
| ⇒ 2ef=24 |
| | 2 | |
oraz e
2+f
2=4a
2 ⇒ (e+f)
2−2e*f=25 ⇒ (e+f)
2=49 ⇒ e+f=
7
8 mar 22:22
Mila:
Dwa razy prosiłam o pełną treść.
Dzięki Eto.
8 mar 22:31
Hektor: Dzięki Eto i Mila ale to jest pełna treść zadania:
Suma długości przekątnych rombu na rysunku obok jest równa:
6
7
8
9
Na rysunku obok jest narysowany romb z wpisanym kołem i zaznaczonym promieniem 1,2cm.
I wciąż nie wiem jak to zrobić.
8 mar 23:54
Hektor: Jak ktoś wpadnie na odpowiedź to niech pisze.
8 mar 23:56
Mila:
Jutro napiszę, wymazałam rozwiązanie tak udziwnionego zadania, sądziłam, że ma być zgodnie z
treścią Ety.
Daj zadanie na wrzutę, chodzi mi o rysunek.
8 mar 23:59
Hektor:
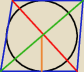
I masz podane że ten promień to 1,2 cm.
9 mar 00:07
Mila:
Cały czas myślę, że o długości boku (2,5 ) masz podaną wcześniej informację.
9 mar 19:07
Hektor: Haha Mila już się nie trudź...
9 mar 22:52
Hektor: Dziś w szkole się dowiedziałem że moja Pani Profesor jak przygotowała zestaw przygotowujący do
testu z geometrii przy rysowaniu tego rysunku nie zaznaczyła na nim boku...
I faktycznie było 2,5.
9 mar 22:54
Hektor: A wczoraj siedziałem nad tym 2 godziny...
9 mar 22:54
Eta:
A nie mówiłam !
9 mar 22:55
Eta:
Pozdrów ode mnie Twoją Panią
9 mar 22:56
Planimetria: Przepraszam za odkopanie tematu, ale skąd wiadomo, ze e2+f2=4a2?
12 sty 16:38
Eta:
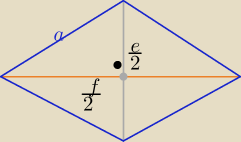
Z tw. Pitagorasa
| f2 | | e2 | |
| + |
| =a2 /*4 ⇒ f2+e2=4a2 |
| 4 | | 4 | |
12 sty 17:04
Planimetria: Aaa no tak, dziękuję
12 sty 18:16