Pytanie do zadania C: Dana jest funkcja f(x)=¹₄x⁴−¹₃x³−⁹₂x²+9x+1, gdzie x∊R a) Wyznacz ekstrema lokalne b) Wyznacz zbiór wartości funkcji Czy mógłby mi ktoś wytłumaczyć dlaczego przy trzech (dobrze wyliczonych) ekstremach f_min(−3), f_max(1) i f_min(3), podany w odpowiedziach zbiór wartości to <f(−3), +∞) ? Przecież funkcja ma maksimum.

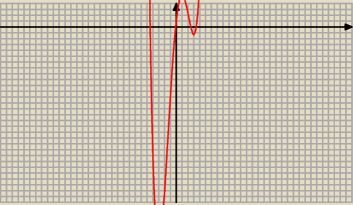
Janek191:: Patrz na wykres

Janek191:: Ma ale maksimum lokalne

C: A jak się tego domyślić nie mając pod ręką programu do rysowania wykresów?

Janek191:: Trzeba policzyć granice w − ∞ i w +∞ Minimum globalne ( w tym przypadku ) , to mniejsza z liczb ( minimów lokalnych ).

Janek191:: lim f(x) = + ∞ x → −∞ i lim f(x) = + ∞ x→ +∞ więc ZW_f = < min_g; + ∞ )

C: Czyli mając za zadanie policzyć zbiór wartości, to zawsze powinnam (oprócz ekstremów lokalnych) liczyć granice tej funkcji w nieskończonościach?

Janek191:: Tak by wypadało

C: Okej, dzięki za pomoc

Janek191:: Oczywiście, gdy D_f = ℛ

C: Wiem, wiem