stożki elcia : rójkat o bokach długości 15,20 i 25 obracamy wokół najdłuzszego boku i otrzymujemy bryłę złożoną z dwóch stożków o wspólnej podstawie. objetość tej bryły jest równa. Wie ktoś jak to zrobic?

elcia : ?

elcia : ?

Patryk: Ze wzoru Herona oblicz pole tego trójkąta, a następnie z pola wylicz wysokość opadającą na najdłuższy bok − będzie to promień podstawy stożka. Następnie korzystając z twierdzenia Pitagorasa oblicz wysokość jednego ze stożka (drugi będzie wynosił 25− ta wysokość), czyli tak: Pole trójkąta: p − połowa obwodu p=(25 + 15 + 20) : 2 = 30 P=√p(p−a)*(p−b)*(p−c) P=√30 * 5 * 10 * 5 = √22500 = 150

	1
P=		*a*h
	2

	1
150 =		* h * 25 / *2
	2

25h=300 h=12

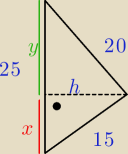
Patryk: Nasze h=r=12 Z tw. Pit. obliczamy wysokość "dolnego" stożka − x x² + 12²=15² x²=225−144 x²=81 x=9 25 − x = y y = 25 − 9 = 16 V − objętość całej bryły

	1		1
V = π * r2 * x *		+ π * r2 * y *
	3		3

	1		1
V = π * 122 * 9 *		+ π * 122 * 16 *		= 1200 π
	3		3

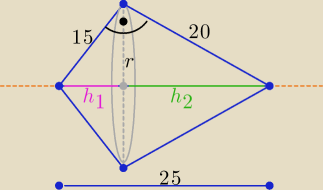
Eta: Ten trójkąt jest prostokątny ( dlaczego?

	15*20
r=		⇒ r= 12
	25

h₁+h₂=25 Taka bryła składa się z dwóch stożków sklejonych podstawami

	1		1		1		1
V(bryły)=		r2*h1+		πr2*h2=		πr2*(h1+h2)=		πr2*25
	3π		3		3		3

V=........... dokończ