Przekształcenia funkcji
Młody: Napisz wzór funkcji g której otrzymamy po przekształceniu względem osi OX:
f(x)=√x−2+1
8 mar 15:00
Janek191::
Jakim przekształceniu ? Symetria osiowa względem OX ?
8 mar 15:02
Młody: Tak
8 mar 15:03
Młody: według mnie to g(x)=−√x−2−1 albo g(x)=√−x+2−1
8 mar 15:06
Janek191::
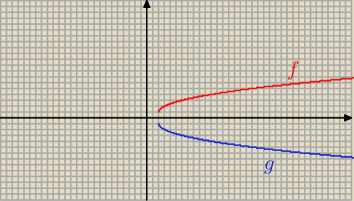
g(x) = − 1*f(x) = −
√x − 2 − 1
8 mar 15:07
Młody : Wykres funkcji f (x)=x2 przesuń równolegle o wektor u=[3,−2].Napisz wzór funkcji g której
wykres otrzymałeś. Pomożesz jeszcze z tym?
8 mar 15:15
Kacper:
g(x)=(x−3)2−2
8 mar 15:16
Młody : Jakim wzorem to zrobiłeś czy jak żebym wiedział jak resztę tego typu zadań robić
8 mar 15:20
Janek191::
f(x) [ p , q ]
g(x) = f( x − p) + q
8 mar 15:27
Młody : Zawsze tym wzorem mam się kierować?
8 mar 15:29
Janek191::
Nie zawsze : Tylko przy translacji o wektor [ p , q ]
8 mar 15:48
Młody : A jak wyglądałby wykres funkcji g?
8 mar 16:16
Janek191::
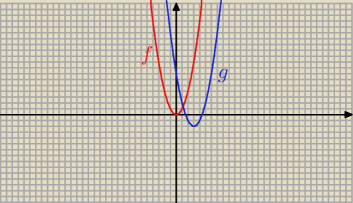
8 mar 16:48
Młody : Na podstawie wykresu funkcji f (x)=|x|−2 naszkicuj wykres funkcji g (x)=| |x|−2|.
8 mar 17:13
Janek191::
Narysuj wykres funkcji f , a następnie odbij symetrycznie część wykresu , która
jest pod osią OX względem tej osi.
8 mar 17:15
Młody : W tym problem że nw jak narysować funkcje f słaby z tego działu jestem
8 mar 17:20
Janek191::
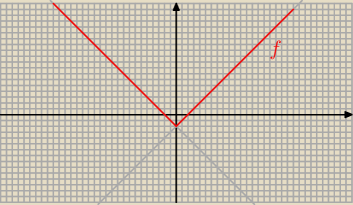
8 mar 17:22
Janek191::
Wykres funkcji h(x) = I x I przesuwamy w dół , czyli o wektor [ 0 ; − 2] i otrzymujemy
wykres funkcji f
8 mar 17:24
Młody : I ostatnie zadanie: Dziedziną funkcji f jest zbior Df=<−4,8>a jej zbierem wartości jest zbiór
ZWf=<−1,+~) Podaj dziedzine i zbiór wartości funkcji g określonej wzorem g (x)=f (−x)
8 mar 17:34
 g(x) = − 1*f(x) = − √x − 2 − 1
g(x) = − 1*f(x) = − √x − 2 − 1

