sin |x| < 1 Kuba: f(x) = sin |x| Rozwiąż nierówność f(x) < 1 dla x ∊ <−π,π> Próbowałem to liczyć jak dla nierówności z wartością bezwględną, ale wynik wychodzi zły.

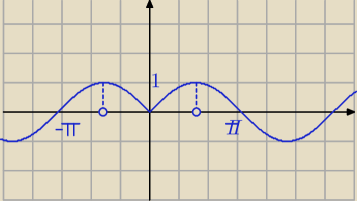
Mila: Odczytaj z rysunku.

Kuba: Z wykresu umiem odczytać. Ale nie wiem czy samo odczytanie było by zaliczone, po za tym przy bardziej skomplikowanych przykładach, już nie będzie takie proste odczytanie/narysowanie wykresu.

Draghan: Przy nierównościach trygonometrycznych i tak bez wykresu się (zazwyczaj) nie obędzie. A taki wykres to przecież pełnoprawne narzędzie do rozwiązania zadania, bo dlaczego nie? Grunt, żeby był poprawny.

prosta: Każdy przykład jest inny ....przy nierównościach trygonometrycznych odwołujemy się do wykresów

Mila: f(x)=sin|x| jest parzysta, zatem równanie ( nierówność) ma w przedziale <−π,0> takie samo rozwiązanie jak sinx<1 w przedziale <0,π> Rozwiązujesz każde równanie stosownie do jego postaci.

prosta: z definicji wartości bezwzględnej też powinno wyjść: 1.gdy x∊<0, π>:

	π		π
sin|x| <1 ⇔ sinx<1 ⇔ x∊<0,		)∪(		,π>
	2		2

2.gdy x∊<−π, 0) :

	π		π
sin|x| <1 ⇔ sin(−x)<1 ⇔ −sinx<1 ⇔sinx>−1 ⇔ x∊<−π,−		)∪(−		,0)
	2		2