aa
Hugo: QULKA

? FIZYKA !
( : Tam ten przyklad przeklepalem do zeszytu
Gaz dwuatomowy o temperaturze 250
oC sprężany jest izotermicznie w ten sposób, że jego objętość
zmniejsza się 3 razy. Następnie w wyniku przemiany adiabatycznej rozszerzył się uzyskując
pierwotne ciśnienie. Znaleźć temperaturę tego gazu na końcu przemiany adiabatycznej.
7 mar 21:04
Hugo: dwu atomowy czyli
n=2

?
t = 250
oC czyli , 250 + 273 = 523 K
V1 = 3V2
potem adiabatycznie i ma to samo ciśnienie

sz. T
k
7 mar 21:21
Hugo: pv = nrt
p1v1 = 2*8,314 * 523
p1v1 = 8696.4
v1 = 3v2
:((?
7 mar 21:23
Hugo: skoro izotermicznie
pv = pv
to ciśnienie sie musialo zmienić tez 3 krotnie
3pv = p3v
a potem adiabatycznie
pvk = p1vk
:((? nie mamy kappy ani nic
7 mar 21:30
kyrtap: pomagam ale nie wiem czy dobrze :
p1 − ciśnienie początkowe
p2 − ciśnienie końcowe
wiemy że p1 = p2 (bo w wyniku adiabaty gaz powrócił do pierwotnego ciśnienia)
V1 − objętość początkowa
V2 − objętość końcowa
V1 = 3V2
T1 − temperatura początkowa
T2 − temperatura końcowa
T1 = 250 + 273 = 523
Przemianę adiabatyczną można zapisać także za pomocą równania stanu gazu doskonałego:
Podstawiam:
p1 *V1 * T2 = 1569 * p1 * V2 / : p1*V1
T2 = 1569 [K]
7 mar 21:42
Hugo: Dz

juz pacze
7 mar 21:43
Hugo: coś za proste

jak to rozwiązujesz
7 mar 22:02
Hugo: myślalem ze bedą tam T1 T2 i T3
7 mar 22:02
Hugo: ale fajne nowe spojrzene z tym równaniem

x = x
7 mar 22:02
kyrtap: Hugo jak za proste to czemu kucu nie rozwiązał?
7 mar 22:03
kyrtap: 
7 mar 22:04
7 mar 22:04
kyrtap: niech wypowiedzą się eksperci

7 mar 22:06
kyrtap: wersja druga ulepszona

Korzystam z Prawa Poissona :
p1*V1
k = p2 * V2
k
gdzie k − współczynnik adiabatyczny dla 2−atomowych gazów k = 1.4
p1 = (1/3)
1.4 teraz to podstaw do wzoru tamtego i chyba powinno być dobrze

7 mar 22:23
Hugo: 
7 mar 22:30
Hugo: Poisson, ze otruty

7 mar 22:30
Hugo: nie rozumiem
pv
k = pv
k
a zniklo p
2
p
2 = 1?
7 mar 22:33
kyrtap: nie jeszcze razy p2, nie dopisałem
7 mar 22:35
Hugo: zatem p
1 = (1/3)
1,4 p
2
do wzoru

p1v1/t1 = p2v2/t2
7 mar 22:37
Hugo: p1V1/5231 = p1* 3V1/T2 (1/3)
1,4
1/523 = 3 /T2 * (1/3)
1,4
T2 = 523 * (1/3)
1,4 * 3
T
2 = 335.766

?
7 mar 22:45
kyrtap: chyba jo

7 mar 22:55
Lukas:
Hugo widziałeś mój rysunek kucu ?

7 mar 22:55
Hugo: fajny xd widzialem
7 mar 23:05
Qulka: 
7 mar 23:09
Hugo: Qulka


!
7 mar 23:09
Hugo: kolejne?

7 mar 23:09
Hugo: Proszę wyprowadzić wzory na pracę dla gazu doskonałego poddanego przemianie:
a) izotermicznej,
b) izobarycznej,
c) adiabatycznej.
jak to zrobic

7 mar 23:10
Qulka: dwuatomowa cząsteczka to rodzaj np. tlen

a dwa mole to ilość

to zdecydowanie NIE to
samo

7 mar 23:11
Hugo: a to nie czasem


pv/t = pv/t i poprostu do a) mnozymy przez t?
7 mar 23:11
Qulka: chwila moment po kolei

7 mar 23:14
Qulka: sprawdzam pierwsze

7 mar 23:15
Hugo: 
7 mar 23:16
Qulka: co wyście nakombinaowali

7 mar 23:18
Hugo: źle

? pomóż prosze

7 mar 23:26
Qulka: izoterma
p1V1=p2V2
p1V1=p2V1/3
p1=p2/3
p2=3p1
adiabata ϰ=1.4
3p1(V1/3)
1.4 = p1Vx
1.4
3(V1/3)
1.4 = Vx
1.4
Vx=0,7306V1
T1(V1/3)
ϰ−1=T2Vx
ϰ−1
| | T1(V1/3)ϰ−1 | |
T2= |
| = T1•1,3687381=715,850 |
| | (0,7306V1)ϰ−1 | |
7 mar 23:28
Qulka:
a) izoterma
b) izobara
W=−p(V2−V1)
c)adiabata
7 mar 23:31
kyrtap: 
7 mar 23:33
Hugo: jj

juz przepisuje Dz Qulka

a jutro kiedy bedziesz



co do zadania tym a)b)c) to mam wzór

i z nich mam tak poprzekształcać by wyszło
odpowiednio
pv = pv
p/t = p/t
v/t = vt ?
7 mar 23:55
Qulka: jutro też nocą

weekendy mam najbardziej zajęte

7 mar 23:57
Hugo: Bo jestem w akademiku a tez nie chce na bezczelnego lokatorom

to spróbujmy jak najwiecej
czyli pewnie max jedno

7 mar 23:59
Hugo: Co do pytania z tymi wzorami

? to tak jak mowie?
a)
| | V2 | |
W = −nRTln |
| =...... = p1V1 = p2V2? |
| | V1 | |
8 mar 00:00
Hugo: tam jest logarytm

jak to by?
8 mar 00:00
Qulka: ale to zupełnie co innego

praca to pole pod krzywą p(V)
8 mar 00:00
Hugo: ;−;
8 mar 00:04
Hugo: Czyli całkujemy to

? by wyprowadzic ten wzor

8 mar 00:04
Hugo: ale wyprowadzic to napisac? tak z nikąd? czy to sie zkąś bierze?
8 mar 00:05
Qulka: tak

8 mar 00:05
Qulka: z Clapeyrona

8 mar 00:05
8 mar 00:09
Qulka: i całkujemy

i będzie logarytm

8 mar 00:09
Hugo: 
aaa
8 mar 00:32
Hugo: a to drugie? b)?
8 mar 00:32
Hugo: co calkuje? i tak samo co do c) co całkuje

?
8 mar 00:32
Hugo: w c) nasuwa mi sie pv
k zeby calkowac ale w b) jest dziwne

8 mar 00:33
Qulka: izobara to stałe ciśnienie więc całkujesz ze stałego p0
8 mar 00:40
Qulka:
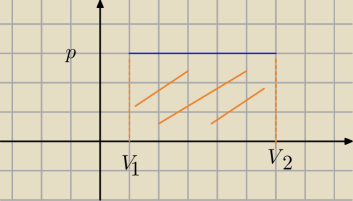
8 mar 00:41
8 mar 00:42
Hugo: CZYLI

calkuje zawsze
pv = nRT tylko stale sie zmieniają



?
8 mar 00:43
Qulka: nie

8 mar 00:44
Qulka: widać obrazek

8 mar 00:44
Hugo: no widac praca to pole
8 mar 00:45
Qulka: w b) całka ∫pdV= pV w granicach od v1 do v2 więc pV2−pV1 = p(V2−V1)
8 mar 00:45
Qulka: ale p jest STAŁE
8 mar 00:45
Hugo: " izobara to stałe ciśnienie więc całkujesz ze stałego p0"
całkuje ? z wzoru pv = nRT?
izobara to V/T = V/T bo p = const
wiec stałe jest p ale v i T nie ? i calkuje po nich

?
8 mar 00:46
Qulka: praca gazu to zawsze POLE POD wykresem p(V)


i tylko p(V)
8 mar 00:47
Hugo: pdf a gdzie jest T?

w izobarycznej T jest zienną
8 mar 00:48
Qulka: całka z CIŚNIENIA po OBJĘTOŚCI
∫ ciśnienie d(objętość) tak jak ∫ A dx
8 mar 00:50
Qulka: a;bo lepiej ∫ 5 dx widać ze stałe

8 mar 00:50
Qulka: tak samo byłoby ∫ 5 dV
8 mar 00:51
Hugo:
;−; jest funkcja p(V) ona sb leci poziomo i jako całka oznaczona ma dolną i górną granice V
1
V
2 dlatego mamy w tym wypadku czworokąt
i to na niebiesko ten prostokąt to pole pracy czyz nie?
8 mar 00:51
Qulka: tak
8 mar 00:53
Qulka: a ten czworokąt to można spokojnie nazwać prostokątem i pole to bok •bok

8 mar 00:54
Hugo: a dlaczego lecimy po objętosci w izobarze

?
8 mar 00:56
Hugo: twierdzisz ze całkujemy po jednej zmiennej w izobarze całka z ∫ V dt
8 mar 00:56
Qulka: wykres p(V) więc i tu i tu i tu ∫ p dV
8 mar 00:58
Hugo: ;−;
8 mar 01:02
Hugo: rysunek jest do izotermy i calkujemy po V a p jest stałą
co do izobary mamy V1/T1 = V2/T2 i calkujemy rowniez po V?
8 mar 01:03
Qulka: w izotermie to była całka z ∫ p dV ale ponieważ p=nRT/V
to ∫ p dV = ∫ nRT/V dV = stałe przed całkę = nRT ∫ 1/V dV = nRT lnV w granicach
8 mar 01:05
Qulka: ODPIERWIASTKUJ się od tych głupich wzorów które są uproszczeniem Clapeyrona tylko po to zeby
sobie przeliczać punkty na krzywej i można je do kosza ciepnąć
8 mar 01:07
Qulka: jeszcze raz od początku wszystko <wwwrrrrrrrrrrr>
8 mar 01:09
Qulka: PRACA to W= ∫ p dV
a) dla izotermicznej, p=nRT/V
więc ∫ p dV = ∫ nRT/V dV = stałe przed całkę = nRT ∫ 1/V dV = nRT lnV w granicach =
nRT(lnV2−lnV1)= nRT ln(V2/V1)
b) izobarycznej, p = stałe
więc ∫ p dV = p ∫dV = p V = w granicach = p(V2−V1)
8 mar 01:13
Hugo: ok , staram sie zrozumieć to wszystko. Zatem izoterma jest zrobiona
Izobara:
W=−p(V2−V1)
lewa strona
Całka z p = W prawda

a prawa strona skąd sie bierze? nie mamy tam stałych nRT
8 mar 01:13
Hugo: czytam...
8 mar 01:15
Hugo: Ok

cos powoli mi świta... ale ... ja nie mam przerobionych calek oznaczonych , mam
przerobione nie oznaczone.
∫ p dV = p ∫dV = p V = w granicach = p(V2−V1)
wyrzucamy p przed calke mamy samo dv
czyli z tego co sie uczylem (na przykladzie x)
całka z niczego czyli 1 czyli ∫ 1 * dx = x

? + C (+ stała)
czyli jak oznaczona całka to x − x? −> v
2 − v
1?

8 mar 01:18
Hugo: CHYBA ZROZUMIALEM

8 mar 01:19
Hugo: 
zawsze sie robi po p by wyszla praca

8 mar 01:20
Qulka: | | p1V1ϰ | |
c) dla adiabatycznej p = |
| |
| | Vϰ | |
| | p1V1ϰ | | 1 | | V−ϰ+1 | |
więc ∫ p dV = ∫ |
| dV = p1V1ϰ ∫ |
| dV = p1V1ϰ |
| |
| | Vϰ | | Vϰ | | −ϰ+1 | |
8 mar 01:21
Qulka: tak

oznaczona to po prostu zamiast stałej wstawiasz za zmienną koniec a potem odejmujesz
z wstawionym początkiem
8 mar 01:22
Hugo: z tym adiabatą sobie jeszcz epomysle, ide spac

dzieki wielkie mądra istoto

! kolorowych
8 mar 01:27
Qulka: adiabaty nie skończyłam..tam trzeba jeszcze wstawić V2 i potem V1 ale też już chyba idę saoć
aaaaaaaaaaaaaaaaaaaa MINUS WSZĘDZIE W= − ∫ pdV
8 mar 01:31
8 mar 01:31
Hugo: czemu minus?
8 mar 14:49
Hugo: ehmm nie rozumiem to jak bys potem byla to prosze wytlumacz

8 mar 15:29
Hugo: (Np. 5/3 – dla gazów jednoatomowych, 7/5 – dla gazów
dwuatomowych, 4/3 – dla gazów wieloatomowych.
fajne

1,66
1,4
1,33
8 mar 15:37
Hugo: co do adiabaty to ok przesledziem jednak troche jasne to jest

ale !
dlaczego sie to wyrzuca przed znak calki?
http://scr.hu/2pdc/9sq81
:((
pV
k 
a tej drugiej nie
8 mar 15:46
Hugo: Temperatura czterech moli dwu atomowego gazu doskonałego wzrosła o ΔT =60
o, w warunkach
stałego ciśnienia. Ile ciepła dostarczono do gazu? O ile wzrośnie energia wewnętrzna gazu?
Jaką pracę wykona gaz?
k = 1,4 bo dwu atomowe
jak

8 mar 16:53
Qulka: bo te z indeksami to stałe czyli jakieś określone p1 V1 a to końcowe to nieokreślone V tak
daleko jak daleko będziesz całkować i ono zostaje do całkowania
9 mar 01:34
Hugo: Qulka jestes?

nie rozumiem troche

22 mar 19:49
Hugo: 7mar 23:28 tam masz kappe −1 , dlaczego ;−;?
22 mar 19:50
Qulka: bo taki jest wzór jak ciśnienie to kappa, jak temp to kappa−1
22 mar 23:38
 ? FIZYKA !
( : Tam ten przyklad przeklepalem do zeszytu
Gaz dwuatomowy o temperaturze 250oC sprężany jest izotermicznie w ten sposób, że jego objętość
zmniejsza się 3 razy. Następnie w wyniku przemiany adiabatycznej rozszerzył się uzyskując
pierwotne ciśnienie. Znaleźć temperaturę tego gazu na końcu przemiany adiabatycznej.
? FIZYKA !
( : Tam ten przyklad przeklepalem do zeszytu
Gaz dwuatomowy o temperaturze 250oC sprężany jest izotermicznie w ten sposób, że jego objętość
zmniejsza się 3 razy. Następnie w wyniku przemiany adiabatycznej rozszerzył się uzyskując
pierwotne ciśnienie. Znaleźć temperaturę tego gazu na końcu przemiany adiabatycznej.
 ?
t = 250 oC czyli , 250 + 273 = 523 K
V1 = 3V2
potem adiabatycznie i ma to samo ciśnienie
?
t = 250 oC czyli , 250 + 273 = 523 K
V1 = 3V2
potem adiabatycznie i ma to samo ciśnienie  sz. Tk
sz. Tk
 juz pacze
juz pacze
 jak to rozwiązujesz
jak to rozwiązujesz
 x = x
x = x





 Korzystam z Prawa Poissona :
p1*V1k = p2 * V2k
gdzie k − współczynnik adiabatyczny dla 2−atomowych gazów k = 1.4
Korzystam z Prawa Poissona :
p1*V1k = p2 * V2k
gdzie k − współczynnik adiabatyczny dla 2−atomowych gazów k = 1.4



 p2 = 1?
p2 = 1?
 p1v1/t1 = p2v2/t2
p1v1/t1 = p2v2/t2
 ?
?




 !
!


 a dwa mole to ilość
a dwa mole to ilość  to zdecydowanie NIE to
samo
to zdecydowanie NIE to
samo 

 pv/t = pv/t i poprostu do a) mnozymy przez t?
pv/t = pv/t i poprostu do a) mnozymy przez t?




 ? pomóż prosze
? pomóż prosze

 juz przepisuje Dz Qulka
juz przepisuje Dz Qulka  a jutro kiedy bedziesz
a jutro kiedy bedziesz

 co do zadania tym a)b)c) to mam wzór
co do zadania tym a)b)c) to mam wzór  i z nich mam tak poprzekształcać by wyszło
odpowiednio
pv = pv
p/t = p/t
v/t = vt ?
i z nich mam tak poprzekształcać by wyszło
odpowiednio
pv = pv
p/t = p/t
v/t = vt ?
 weekendy mam najbardziej zajęte
weekendy mam najbardziej zajęte 
 to spróbujmy jak najwiecej
czyli pewnie max jedno
to spróbujmy jak najwiecej
czyli pewnie max jedno 
 ? to tak jak mowie?
a)
? to tak jak mowie?
a)
 jak to by?
jak to by?
 praca to pole pod krzywą p(V)
praca to pole pod krzywą p(V)
 ? by wyprowadzic ten wzor
? by wyprowadzic ten wzor


 i będzie logarytm
i będzie logarytm 
 aaa
aaa
 ?
?


 http://pl.wikipedia.org/wiki/Przemiana_adiabatyczna
http://pl.wikipedia.org/wiki/Przemiana_adiabatyczna
 calkuje zawsze
pv = nRT tylko stale sie zmieniają
calkuje zawsze
pv = nRT tylko stale sie zmieniają

 ?
?


 ?
?

 i tylko p(V)
i tylko p(V)
 w izobarycznej T jest zienną
w izobarycznej T jest zienną

 ;−; jest funkcja p(V) ona sb leci poziomo i jako całka oznaczona ma dolną i górną granice V1
V2 dlatego mamy w tym wypadku czworokąt
i to na niebiesko ten prostokąt to pole pracy czyz nie?
;−; jest funkcja p(V) ona sb leci poziomo i jako całka oznaczona ma dolną i górną granice V1
V2 dlatego mamy w tym wypadku czworokąt
i to na niebiesko ten prostokąt to pole pracy czyz nie?

 ?
?
 a prawa strona skąd sie bierze? nie mamy tam stałych nRT
a prawa strona skąd sie bierze? nie mamy tam stałych nRT
 cos powoli mi świta... ale ... ja nie mam przerobionych calek oznaczonych , mam
przerobione nie oznaczone.
∫ p dV = p ∫dV = p V = w granicach = p(V2−V1)
wyrzucamy p przed calke mamy samo dv
czyli z tego co sie uczylem (na przykladzie x)
całka z niczego czyli 1 czyli ∫ 1 * dx = x
cos powoli mi świta... ale ... ja nie mam przerobionych calek oznaczonych , mam
przerobione nie oznaczone.
∫ p dV = p ∫dV = p V = w granicach = p(V2−V1)
wyrzucamy p przed calke mamy samo dv
czyli z tego co sie uczylem (na przykladzie x)
całka z niczego czyli 1 czyli ∫ 1 * dx = x  ? + C (+ stała)
czyli jak oznaczona całka to x − x? −> v2 − v1?
? + C (+ stała)
czyli jak oznaczona całka to x − x? −> v2 − v1? 

 zawsze sie robi po p by wyszla praca
zawsze sie robi po p by wyszla praca 
 oznaczona to po prostu zamiast stałej wstawiasz za zmienną koniec a potem odejmujesz
z wstawionym początkiem
oznaczona to po prostu zamiast stałej wstawiasz za zmienną koniec a potem odejmujesz
z wstawionym początkiem
 dzieki wielkie mądra istoto
dzieki wielkie mądra istoto  ! kolorowych
! kolorowych

 1,66
1,4
1,33
1,66
1,4
1,33
 ale !
dlaczego sie to wyrzuca przed znak calki?
http://scr.hu/2pdc/9sq81
:((
pVk
ale !
dlaczego sie to wyrzuca przed znak calki?
http://scr.hu/2pdc/9sq81
:((
pVk  a tej drugiej nie
a tej drugiej nie

 nie rozumiem troche
nie rozumiem troche