optymalizacja, odległość punktu od prostej delta_is_love/life: wyznacz współrzędne punktu P należącego do wykresu funkcji f i leżącego najbliżej prostej x−y+2=0: a) f(x)= 1−x² odp.: (−¹₂;³₄) mój tok rozwiązywania: 1. współrzędne pkt. P(x; 1−x²) 2. podstawiam wartości pod wzór na odległość pkt. od prostej; 3. wyznaczam pochodną optymalizowanej odległości 4. wyznaczam wierzchołek wykresu pochodnej (bo jest to f. kwadratowa) 5. podstawiam x wierzchołka do wspólrzędnych pkt P. i otrzymuje błędny wynik. czy problem tkwi w toku rozwiązywania? proszę o pomoc

===: ... a do czego Ci wierzchołek pochodnej ?

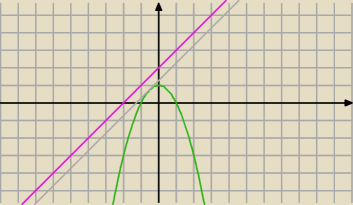
===: łatwiejszy sposób to poszukać punktu należącego do f(x) w którym pochodna jest równoległa do danej prostej Prosta y=x+2 Pochodna f'(x)=−2x −2x_s=1 ⇒ x_s=−1/2 y_s=1−1/4=3/4