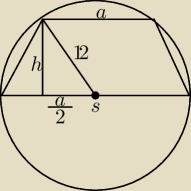
zadanie optymalizacyjne anonek: Bardzo proszę o pomoc! Rozpatrujemy wszystkie trapezy, wpisane w okrąg o promieniu 12 w taki sposób, że podstawa trapezu jest średnicą okręgu. Oblicz długości boków tego z rozpatrywanych trapezów, który ma największe pole. wyliczam z pitagorasa zależność między a i h 144=h²+^a₂⇒h=√144−^a2₄ zapisuje wzór funkcji p(a)=^a₂*√144−^a2₄+12*√144−^a2₄ ustalam dziedzinę funkcji D_p∊(0;24) p(a)=√^a2₄(144−^a2₄)+√144(144−^a2₄) I tu pojawia się problem, mianowicie pochodna funkcji p oraz moje pytanie jak ją obliczyć? Jako pochodną funkcji złożonej dodać pochodna drugiej funkcji złożonej?

===: masło maślane a maślane masło Ty założyłeś z mety jaki to trapez więc niby po co te pochodne − Wytłumacz mi proszę dlaczego to pierwsze założenie, że 144=h²+(a/2)²

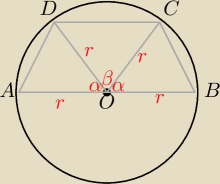
Raf131: dokładnie za szybko wszystko. Na razie mamy tylko informację o tym, że wpisujemy dowolny trapez w okrąg, którego dłuższa podstawa jest średnicą. Druga podstawa trapezu może pokrywać się z różnymi cięciwami okręgu. Patrz rysunek Czy już widzisz?