DOWÓD GEOMETRYCZNY nudnyhobbit: W trójkącie ABC dana jest środkowa CD. Z punktu D poprowadzono środkową DE trójkąta ADC oraz środkową DF trójkąta CDB. Wykaż, że jeśli |DE| = |DF| to trójkąt ABC jest równoramienny.

Eta:

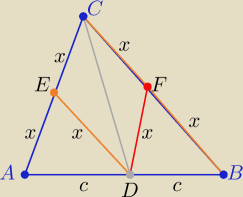
	1		1
|ED|=		|BC| i |DF|=		|AC| ( dlaczego? napisz uzasadnienie
	2		2

z założenia |DE|=|DF| to |AC|=|BC|=2x zatem trójkąt ABC jest równoramienny