zadanko
optymalizant: hej,
"Wyznacz równanie prostej przechodzącej przez punkt A(−2,−1) i przecinającej ujemne półosie
układu współrzędnych w takich punktach, których suma odległości od początku układu
współrzędnych jest najmniejsza. "
proszę o pomoc, chciałem zrobić to tak, że biorę prostą przechodzącą przez 0,0 oraz punkt A i
znaleźć do niej prostą prostopadłą, ale w sumie to nie ma sensu, bo w niczym mi to tutaj nie
pomoże. proszę o pomoc.
7 mar 17:30
optymalizant: założenia x<0, y<0
7 mar 17:30
optymalizant: ktoś wie?

7 mar 17:57
optymalizant: αβδγ
7 mar 19:16
optymalizant: α∞≤∊∫
7 mar 19:58
8 mar 01:22
Qulka:
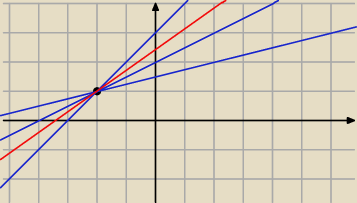
8 mar 01:29
optymalizant: nie do końca, bo ma przecinać ujemne półosie..jak to znaleźć? próbowałem chyba wszystkiego, za
nic nie mogę dojść, choć zadanie wydaje się proste.
8 mar 01:33
Qulka: a to już poprawiam

8 mar 01:35
Qulka:
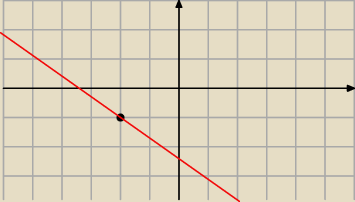
8 mar 01:39
Qulka: i suma odległości wynosi 3+2√2
8 mar 01:41
pigor: ..., teraz idę spać, ale jak ... wstanę, to
zaproponuję jego rozwiązanie (...

widzę już je) .
8 mar 01:44
pigor: ... o

już coś jest , zobaczymy co mi ...

wyjdzie ; dobranoc
8 mar 01:47
Qulka: jak mi −1 wskoczyła nad oś to tak wyszło

8 mar 01:51
Qulka: ja wzięłam założenie, że szukasz min |−b/a| +|b| a ponieważ obie ujemne to wyszło b/a −b
i jednocześnie −1=−2a+b więc b=2a−1
8 mar 01:54
optymalizant: dziękuję, wstanę rano, przeczytam i przeanalizuję, teraz się położę, bo już mózg nie pracuje
tak jak powinien

8 mar 01:56
optymalizant: oki, jestem, ale nadal nie czaję; jak mam znaleźć najmniejszą sumę odległości?
8 mar 14:42
PW: Równanie w postaci kierunkowej
y = ax + b
przy założeniu, że a≠0 i b≠0 − prosta nie jest równoległa do osi OX i nie przechodzi przez
(0,0) − można zapisać jako
i po przyjęciu odpowiednich oznaczeń
Jak łatwo zauważyć, w równaniu (1) x
0 i y
0 oznaczają odpowiednio punkty, w których prosta
przecina osie OX i OY. Jest to tak zwane
równanie odcinkowe prostej (x
0 pokazuje koniec
odcinka wyznaczonego na osi OX, a y
0 − koniec odcinka na osi OY; początkami tych odcinków są
punkty zerowe obu osi).
Jeżeli wyliczymy jakie równania odcinkowe mają proste przechodząca przez zadany punkt (−2, −1),
to odpowiedź będzie łatwa.
Podstawmy więc x = −2 i y = −1 do równania (1):
x
0 = − 2y
0 − x
0y
0
x
0 = − y
0(x
0+2)
Suma S odległości o których mówi zadanie jest równa
(3) S = |x
0|+|y
0| = − x
0 − y
0,
co wynika z założenia, że x
0 i y
0 są liczbami ujemnymi (od tego chyba
powinniśmy zacząć
rozwiązanie).
Podstawienie (2) do (3) daje
Z treści zadania wiemy, że x
0∊(−
∞, −2).
Badanie funkcji
| | x | |
S(x) = −x + |
| , x∊(−∞,−2) |
| | x+2 | |
powinno dać odpowiedź.
8 mar 15:53
pigor: ...,wyznacz równanie prostej przechodzącej przez punkt A=(−2,−1)
i przecinającej ujemne półosie układu współrzędnych w takich punktach,
których suma odległości od początku układu współrzędnych jest najmniejsza.
−−−−−−−−−−−−−−−−−−−−−−−−−−−
otóż w szufladzie mojej Maji widzę to np. tak :
szukam równania kierunkowego prostej
y=ax+b takiego, że
−1=−2a+b i
a<0 i b<0 i funkcja sumy
s(a,b)=|−
ba |+|b|=
ba−b
gdzie (*)
b=2a−1 , czyli s(a)=
2a−1a −2a+1= 2−a
−1−2a+1 ⇔
⇔
s(a)=3−a−1−2a i ma wartość najmniejszą ,jeśli jej pochodna
s' (a)=a
−2−2=0 i s'' (a)= −2a
−3 >0, czyli 1−2a
2=0 ⇒
⇒ a
2=
12=
24 i a<0 ⇒
a=− 12√2 i s'' (−
12√2) >0, więc
z (*)
b= −√2−1 i s(a,b)= s(
− 12√2, −√2−1) = s
najmniejsza,
a wtedy szukane równanie kierunkowe prostej
y= − 12√2 x −√2−1 /*2 ⇔
⇔
√2x+2y+2+2√2=0 − równanie w postaci ogólnej tej prostej. ...

8 mar 18:30
Pudzio: " i funkcja sumy s(a,b)=|− ba |+|b|= ba−b " zawsze gdy zapisuje punkty przecięcia
się prostej z osiami układu współrzędnych zapisuję pod wartością bezwzględną ?
dlaczego potem gdy zdejmuje wartość bezwzględną z |− ba| i dodaję |b| po zanku równości
odejmuję "b" a nie je dodaje ?
28 maj 09:31
Pudzio: ?
29 maj 19:42
Pudzio: .
31 maj 20:27







 ?
?



 widzę już je) .
widzę już je) .
 już coś jest , zobaczymy co mi ...
już coś jest , zobaczymy co mi ... wyjdzie ; dobranoc
wyjdzie ; dobranoc


