Która z podanych funkcj nie ma ekstremów. zad. zamknięte varann: Która funkcja nie ma ekstremów?

	1
y =		3
	2

y = 5x³ + x² + x y = x⁴ − 2 y = |x| Da się to jakoś szybko poznać bez rysowania każdej pochodnej? Wydaje mi się, że ostatnia nie ma ekstremów.

Janek191::

	1
y =(		)3 − nie ma ekstremum − funkcja stała
	2

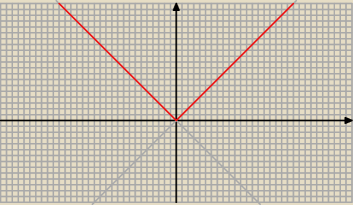
Janek191:: f(x) = I x I

varann: Zapomniałem o X. Tam oczywiście jest 1/2x do potęgi 3. Z tego rysunku wynika, że nie ma ekstrmum dla |x| dobrze rozumiem?

Janek191:: Funkcja y = I x I ma ekstremum − minimum dla x = 0

Draghan: Nie wiem, na ile moje rozumowanie można uznać za poprawne, ale dla funkcji f(x) = |x|, jej pierwsza pochodna nie ma miejsc zerowych − dla x = 0 f'(x) nie istnieje.

PW: Tak jest, pochodna nie istnieje w zerze, nie można więc dla tego punktu stosować twierdzeń, które w założeniu mają istnienie pochodnej. Jest za to oczywiste, że f(0) = f_min (bo z prawej strony zera ma wartości dodatnie, a z lewej też dodatnie), jest więc |0| = 0 = f_min − funkcja ma minimum w zerze i jest ono równe zeru.

Draghan: Dziękuję za wyjaśnienie.