Wyznacz d0mqq: Wyznacz wartość największą i wartość najmniejszą funkcji danej wzorem f(x)= −2/3x²+6 w przedziale <−1;3>. Prosze o wytłumaczenie

Janek191::

	2
f(x) = −		x2 + 6 < − 1; 3 >
	3

p = 0 ∊ < − 1; 3 > q = 6 Obliczamy

	2		2		1
f(− 1) = −		*(−1)2 + 6 = 6 −		= 5
	3		3		3

	2
f( 3) = −		*32 + 6 = − 6 + 6 = 0
	3

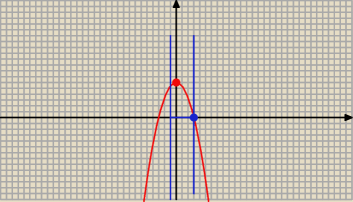
więc y_max = q = 6 y_min = 0 Patrz też wykres

d0mqq: a q nie bedzie równe 3/2?

d0mqq: Aaaaa, źle podstawiłam, zamiast Δ dałam √Δ

d0mqq: a co nam daje oblicznie f(− 1)?

Janek191::

	2
a = −		< 0 , więc ymax = q = f(p) , jeżeli p ∊ < − 1 ; 3 >
	3

Dla x ≠ p jest f(x) < q Sprawdzamy, która z liczb f(−1) , f(3) jest mniejsza

d0mqq: Już rozumiem, dziękuję baaaardzo!