zespolone Magik: Mam problem z l.zespolonymi.oto 3 zadania: http://sendfile.pl/pokaz/271750---gpei.html http://sendfile.pl/pokaz/271751---jD43.html Zna ktoś odpowiedź? Nie wiem jak sie zabrać za to ...

Magik: nikt nic?

Mila: Nie mogę odczytać.

Janek191:: @Mila Kliknij na : podgląd obrazu

prosta: w pierwszym : A ( na 98%)

Magik: Dokładnie tak jak Janek 191 mówi Niestety nie znam hostingów innych ,jak i za bardzo tego działu,jakieś proste rzeczy okej ,ale nie to co dałem wyżej

Magik: ktoś coś,reszte zna ? ⇒

Magik: Mila pomożesz?

Mila: 1) z₀=(√3,√3) A 2)

prosta: 2. wydaje mi się, że jedyne sensowne to A

Mila: a) |7√7−z|≤4 ⇔ |z−7√7|≤4 koło , S=(7√7,0) r=4 Możesz to rozpisać, jeśli nie znasz interpretacji takigo zapisu. z=x+iy |x+iy−7√7|≤4 |(x−7√7)+iy|≤4 √(x−7√7)²+y²≤4 /² (x−7√7)²+y²≤4² Jasne? Czyli zbiór niepusty.

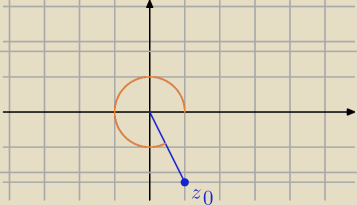
Mila: b) z₀=(1,−√3)

	1		1		3π
cosα=		=		i α>
	√12+√32		2		2

	−√3
sinα=
	2

nieprawdziwa nierówność

prosta: 3. odp. A

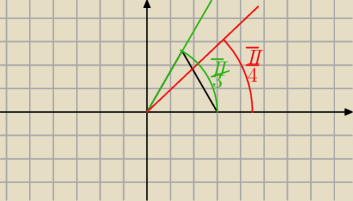
Mila: c) nieprawdziwa nierówność Jak mogłoby by być?

Mila: d) |z−πi|=−1+i Zbiór pusty , wiesz dlaczego? e) tak samo

Magik: Wow,Mila jesteś wielka, dziękuję za pomoc, po narysowaniu i zobrazowaniu tego jest wszystko jasne ,fakt w 2 a) to okrąg,nie zauważyłem tego

prosta: 2d) 2e) to miałoby jakiś sens gdyby po prawej stronie wystąpiła liczba rzeczywista....czy tak?

Mila: Tak.

Magik: W ostatnim prawidłowa odp. to b)

prosta: tak, racja

Magik: Jeszcze mam takie: 1.Ile rozw ma równanie: sprze z=z² z=0 i z=1 więc 2 rozwiązania tak?

Mila: ź=z² (x−iy)=(x+iy)², x,y∊R x−iy=x²+2xyi−y² x−iy=(x²−y²)+2xyi x=x²−y² 2xy=y⇔ 2xy−y=0 y(2x−1)=0

	1
y=0 lub x=		podstawiam do pierwszego
	2

x=x²−0⇔x²−x=0 x=0 lub x=1 (0,0) , (1,0) lub

1		1
	=		−y2
2		4

brak rozwiązań odp z=0 lub z=1

Mila: W ostatnim po podstawieniu do równania mam: |e^2iφ+e^−2iφ|=1⇔

	e2iφ+e−2iφ		1
|		|=
	2		2

teraz znowu nie chcą się pokazać odpowiedzi .