Obliczanie prędkości Davies.: Samochód przejechał 2/3 trasy liczącej 360 km ze stałą prędkością v, a pozostały odcinek trasy przebył z prędkością o 30 km/h większą. Ile czasu jechał z prędkością v, jeśli pokonanie całej trasy zajęło mu 5h 20min. ?

Dobra rada: fizyka.pisz.pl wiesz jaki jest wzór na prędkość ?

Davies.: Wiem, piszę tutaj bo akurat to zadanie mam na matmie

Dobra rada: no to zmienię pytanie: umiesz obliczać ułamki? i zamieniać minuty w godziny

Dobra rada: oraz rozwiązywać układy r−ń

2/3 360
	= v
t1

1/3 360
	= v +30
t2

	1
t1 + t2 = 5		h
	3

Davies.: Miałem problem ułożeniem odpowiedniego układu, dzięki.

pigor: ..., s=vt , to

	240
t1= s1 : v = 23*360 : v =		=? − szukanyczas ,
	v

a z warunków zadania :

	20		240		120		1
t1+t2= 5		⇒		+		= 5		/ : 8 ⇒
	60		v		v+30		3

	30		15		2
⇒		+		=		/ * 3v(v+30) ⇒ 90(v+30)+45v= 2v(v+30) ⇒
	v		v+30		3

⇒ 90v+2700+45v= 2v²+60v ⇒ 2v²−75v−2700= 0 , Δ_v= 75²+8*2700= 75²+36*75= 75*111 ⇒ 5√333 brzydka Δ, może ktoś mnie sprawdzi . ...

prosta: ja napiszę układ:

	16
t1v=240 i (		−t1)(v+30)=120
	3

	240		16		240
t1=		⇒ (		−		)(v+30)=120
	v		3		v

. . . 2v²−75v−2700=0 √Δ=165

pigor: ..., o kurde, liczyłem i ... no tak Δ= 75*75+8*36*75= = (288+75)*75= 363*3*25= 1089*25, to √Δ= 33*5= 165.. .

Dobra rada: oj nie tak kochani, nie tak 240 = vt₁ 120 = vt₂ + 30 t₂ 3(t₁ + t₂) = 16

	240
szukamy właściwie tylko t1 więc z pierwszego r−nia wyznaczamy: v =
	t1

	16−3t1
a z trzeciego: t2 =
	3

i podstawiamy do drugiego: 3t₁² +20t₁ − 128 = 0, √Δ = 44 Odp. t₁ = 4 h

prosta: z naszych obliczeń: v=60km/h ⇒ t₁=4h co jest nie tak ?

pigor: .., no właśnie , a wystarczy przeczytać np. moje rozwiązanie, pasujące do działu funkcje wymierne , lub kolegi ze... zrozumieniem .

Dobra rada: a kto tutaj co czyta...w dodatku ze zrozumieniemP każdy tkwi w największym samozachwycie na swoimi wypocinami...ja również miłej niedzieli z dala od kobiet

prosta: oba rozwiązania pasują do działu : funkcje wymierne....czasami łatwiej policzyć najpierw v, a potem t..... niekoniecznie trzeba budować równanie wymierne z niewiadomą t ( trudniejsze w rozwiązaniu dla przeciętnego maturzysty...) ..ech..idę świętować 8 marca

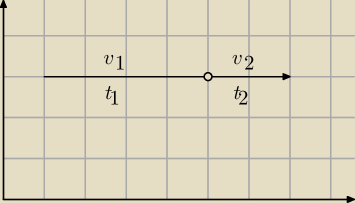
Dziadek Mróz: s = 360 km

	2
s1 =		s = 240 km
	3

	s1
v = v1 =
	t1

	1
s2 =		s = 120 km
	3

	s2
v2 = v1 + 30 =
	t2

	1
t = t1 + t2 = 5h 20m = 5		h
	3

	1
t1 = 5		− t2
	3

s₁, s₂, t₁, t₂, v₁, v₂ ≥ 0

⎧	v1 = s1/51/3 − t2
⎩	v1 + 30 = s2/t2

⎧	v1 = 240 * 3/16 − 3t2
⎩	v1 + 30 = 120/t2

⎧	v1 = 720/16 − 3t2
⎩	v1 + 30 = 120/t2

720		120
	+ 30 =
16 − 3t2		t2

720		120
	−		= −30
16 − 3t2		t2

720t2 − 120(16 − 3t2)
	= −30
t2(16 − 3t2)

720t₂ − 120(16 − 3t₂) = −30t₂(16 − 3t₂) 24t₂ − 4(16 − 3t₂) = −t₂(16 − 3t₂) 24t₂ − 64 + 12t₂ = −16t₂ + 3t₂² −3t₂² + 52t₂ − 64 = 0 3t₂² − 52t₂ + 64 = 0 Δ_t2 = 2704 − 768 = 1936

	52 ± 44		2(13 ± 11)		2
t21/2 =		=		=		(13 ± 11)
	6		3		3

	2		2
t21 =		(13 + 11) =		* 24 = 16
	3		3

	2		4
t22 =		(13 − 11) =
	3		3

	720		720
v11 =		=		< 0 sprzeczność
	16 − 3t21		16 − 3*16

	720		720		720		720
v12 =		=		=		=		= 60
	16 − 3t22		4   16 − 3*   3		16 − 4		12

	4		1
t2 =		= 1		= 1h 20m
	3		3

	km
v1 = 60
	h

pigor: ..., no to jesteśmy kwita i przyznaję , że Dobra rada, bezpośredniego obliczenia czasu to bardzo dobra ... porada, a dzięki temu zainteresowani mają w czym wybierać...