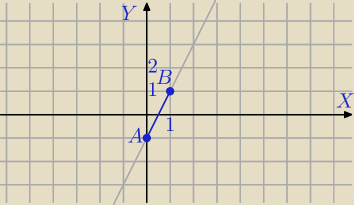
Jak w tekście Michał: Oblicz dla jakich wartości parametru m prost l o równaniu 2x−3y+m=0 ma punkt wspólny z odcinkiem AB, gdy A(0,−1), B(1,1) Tyle j zrobiłem.

	2		2
Policzyłem y=		x +		m
	3		3

	m
−1=		m=−3
	3

	2		m
1=		+		m=1
	3		3

wzór prostej AB=2x−1 Rozwiązaniem jest przedział <−3,1> i tu pojawia się moje pytanie dlaczego powstaje taki przedział ? Czy istnieją jakieś założenia do tego zadania ? Ja uznałem wartość m=−3 i m=1 tak jakby wartościami skrajnymi, a wynik ten pokrywa się z odpowiedzią. Moje rozumowanie jest dobre, czy złe ? Bo nie jestem pewien tego.

Tadeusz: już równanie prostej do postaci kierunkowej przekształciłeś z błędem

Mila: 1) 2x−3y+m=0 ⇔3y=2x+m

	2		m
y=		x+
	3		3

2) prosta AB: y=2x−1 3) punkt przecięcia prostych:

	2		m
2x−1=		x+		⇔
	3		3

4		m
	x=		+1 /*3
3		3

4x=m+3

	m+3
x=
	4

	m+3
0≤x≤1⇔0≤		≤1 /*4
	4

0≤m+3≤4 /−3 −3≤m≤1

Saizou :

	2		1
l:2x−3y+m=0⇒y=		x+		m
	3		3

piszemy równanie prostej AB szukamy punktów przecięcia z prostą l i na koniec stosujemy fakt że ten punkt przecięcia ma leżeć na odcinku AB

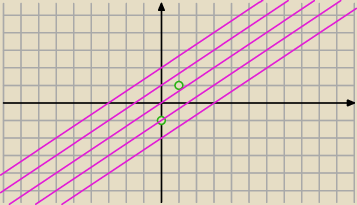
Tadeusz: o prostej 2x−3y+m=0 wiesz, że ma współczynnik kierunkowy a=2/3 Narysowałem Ci kilka prostych o takim współczynniku mających różne b Masz wybrać skrajne, które jeszcze mają punkt wspólny z odcinkiem